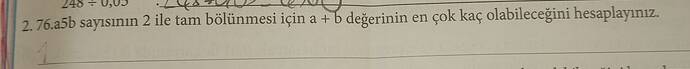76.a5b Sayısının 2 ile Tam Bölünmesi İçin a + b Değerinin En Çok Kaç Olabileceğini Hesaplayınız
Çözüm:
Bir sayının 2 ile tam bölünebilmesi için son basamağının çift sayı olması gerekir. Dolayısıyla, 76.a5b sayısının b basamağı çift bir sayı olmalıdır: 0, 2, 4, 6, veya 8.
Şimdi, her bir çift sayı değeri için (a + b) toplamının en yüksek olabileceği durumu inceleyelim:
- b = 0: (a + 0 = a)
- b = 2: (a + 2 = a + 2)
- b = 4: (a + 4 = a + 4)
- b = 6: (a + 6 = a + 6)
- b = 8: (a + 8 = a + 8)
Burada a’nın en büyük değerini alması gerekiyor ki (a + b) en fazla olsun. a’nın maksimum değeri 9 olabilir.
Hesaplayalım:
- b = 0 için: (a + b = 9 + 0 = 9)
- b = 2 için: (a + b = 9 + 2 = 11)
- b = 4 için: (a + b = 9 + 4 = 13)
- b = 6 için: (a + b = 9 + 6 = 15)
- b = 8 için: (a + b = 9 + 8 = 17)
Sonuç:
(a + b) değerinin en çok olması için, b’nin 8 ve a’nın 9 olması gerekir. Bu durumda, (a + b = 9 + 8 = 17) olur.
O zaman cevap: 17.