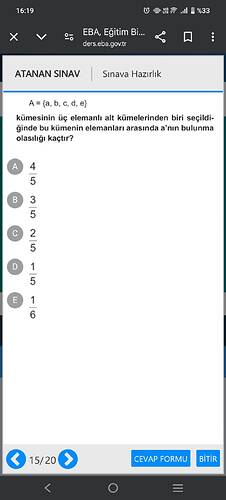
A = {a, b, c, d, e} kümesinin üç elemanlı alt kümelerinden biri seçildiğinde bu kümenin elemanları arasında a’nın bulunma olasılığı kaçtır?
Temel Kavram
Olasılık, belirli bir olayın gerçekleşme olasılığının matematiksel ifadesidir. Belirli bir alt kümenin seçilmesi ve bu alt kümede bir elemanın bulunması gibi durumlarda, kombinatorik hesaplamalar yapılır.
Adım Adım Çözüm
Adım 1: Toplam Alt Küme Sayısını Belirleme
5 elemanlı bir kümeden 3 elemanlı alt kümeler oluşturmanın toplam sayısını belirlemek için kombinasyon formülü kullanılır:
[
C(5,3) = \frac{5!}{3!(5-3)!} = \frac{5 \times 4}{2 \times 1} = 10
]
Adım 2: a Elemanını İçeren Alt Kümeleri Bulma
a elemanını içeren 3 elemanlı alt kümeleri bulmak için geri kalan 4 elemandan 2 tanesini seçmemiz gerekiyor. Bu da yine kombinasyon formülü ile hesaplanır:
[
C(4,2) = \frac{4!}{2!(4-2)!} = \frac{4 \times 3}{2 \times 1} = 6
]
Adım 3: Olasılığı Hesaplama
a elemanının alt kümeler arasında bulunma olasılığı, a’yı içeren alt kümelerin sayısının toplam alt küme sayısına oranıdır:
[
P(\text{a bulunma olasılığı}) = \frac{\text{a bulunan alt küme sayısı}}{\text{toplam alt küme sayısı}} = \frac{6}{10} = \frac{3}{5}
]
Sonuç
a’nın bulunma olasılığı \frac{3}{5}.
Seçeneklerde B şıkkı doğru cevaptır.