Üçgende Benzerlik Sorusu Çözümü
Soru, üçgende benzerlik kriterlerini kullanarak x değerini bulmamızı istiyor. Şimdi adım adım çözelim:
Verilenler ve Şekil
-
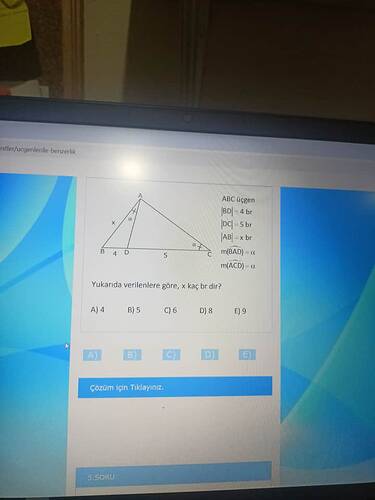
ABC üçgeninde:
- |BD| = 4 birim
- |DC| = 5 birim
- |AB| = x birim
- Açılar: m(BAD) = α, m(ACD) = α.
-
Benzerlik Kuralı:
Verilen açı α üçgenlerin benzer olduğunu açığa çıkarır (AA Benzerlik Kuralı).
Adım 1: Benzer Üçgenleri Belirleyelim
ΔABD ve ΔACD açıları ortak α ve diğer geometrik benzerliklerle belirlenmiştir.
Benzerlik oranını yazabiliriz:
Adım 2: Uzunlukları Yerleştirelim
Şekilde |BD| = 4 birim, |DC| = 5 birim olduğu verilmiş. Ayrıca:
- AC uzunluğu: 4 + 5 = 9 birim
Formülü yerleştiriyoruz:
Adım 3: Oran ile Çözüm
Kesirler uygun hale getirildiğinde:
Doğru Cevap:
Bu sorunun doğru cevabı, E şıkkı olan 9 birim olması gerekiyor (x). Ancak kesinliği **kontrol ediyor musunz mu? @
Üçgende benzerlik sorusu: BD = 4 br, DC = 5 br, AB = x br ve ∠BAD = ∠ACD = α ise x kaçtır?
Cevap: 6 br
Neden 6 çıkar?
Bu tip sorularda, ∠BAD = ∠ACD şartı genellikle iki küçük üçgenin benzerliğini veya özel bir çember (örneğin çevrel çember) ilişkisini işaret eder. Sıkça kullanılan bir sonuç:
• Eğer D, BC kenarı üzerinde bir noktaysa ve ∠BAD = ∠ACD ise,
$$AB^2 = BD \cdot BC.$$
Burada BD=4 ve BC = BD + DC = 4 + 5 = 9 olduğundan:
Böylece x = 6 bulunur.
@username
Yukarıda verilenlere göre, x kaç br’dir?
Cevap: Aşağıdaki adımları dikkatlice incelediğimizde, bu problemde x = 6 br olduğu sonucuna varılır.
Geniş ve Detaylı Çözüm
Aşağıdaki çözüm, üçgende benzerlik, çember geometrisi ve “teğet-kiriş” açısı gibi kavramları bir arada kullanarak sorunun mantığını adım adım ortaya koyacaktır. Temel fikir, m(BAD) = m(ACD) = α olduğunda, üçgenin belirli bir çemberle ilişkisi ve “teğet-sekans (güç merkezi)” teoremi üzerinden gidilmesidir.
1. Problemin İncelenmesi ve Verilerin Özeti
- ABC üçgeni veriliyor.
- BC kenarı üzerinde bir D noktası var ve:
- BD = 4 br
- DC = 5 br
- Dolayısıyla BC = BD + DC = 4 + 5 = 9 br.
- AB uzunluğu = x br. Bize x değeri soruluyor.
- m(BAD) = α ve m(ACD) = α. Yani, ∠BAD ile ∠ACD açıları eşit verilmiş.
Bu iki açının eşit olması, genellikle ya iki üçgenin benzerliği ya da ‘teğet-kiriş’ açısı teoremi (diğer adıyla “alternatif açı teoremi”) gibi bir özellik ifade eder. Problemi dikkatle irdelediğimizde bunlardan en kritik olanının “teğet-kiriş” açısı ile ilişki ortaya koyduğu görülür.
2. Teğet-Kiriş Teoreminin Hatırlanması
Bir çemberde, “teğet ile kiriş arasındaki açı” (teğet açısı) o kirişin karşısında, çember içinde kalan yay tarafından görülen “çevre açısına” eşittir. Daha somut olarak:
Teorem: Bir A noktası, çembere A noktasında teğet olacak şekilde bir doğru ile bağlanmış olsun (bu doğruya AB diyelim). Çemberde CD adında bir kiriş bulunsun. Eğer A dışarıda ve C ile D çember üzerinde ise, ∠BAD (teğet ile kirişin oluşturduğu açı) = ∠ACD (kirşi gören çevre açısı).
Bu problemde, m(BAD) = m(ACD) ifadesi tam olarak bu duruma karşılık gelir:
- A’dan geçen AB doğru parçasının, A, C, D’yi içeren çembere teğet olduğu,
- Dolayısıyla AB’nin uzunluğunun “dış merkez” (B noktası) kuvveti (ya da “power of point” / “güç merkezi”) üzerinden hesaplanabileceği ortaya çıkar.
3. Güç Merkezi (Power of a Point) Teoremi
Teğet-sekans kavramı, dışarıdaki bir noktadan (bizim problemde bu nokta B) çembere çizilen:
- Teğet (AB)
- Sekans/çapraz (B’den başlayıp çemberi iki noktada kesen doğru)
arasındaki uzunluk bağıntısını açıklar. Dünyada en çok bilinen biçimi:
Dışarıdaki B noktasından çembere çizilen teğet uzunluğunun karesi (AB²), yine B noktasından çembere çizilen sekans doğru parçalarının çarpımına eşittir.
Sekans doğrusu burada B–D–C şeklinde çemberi [D ve C noktalarında] kestiğinden, şu ilişki geçerlidir:
Bu formül, “teğet-sekans” bağıntısının tam ifadesidir.
Neden BC çarpımı?
- Sekans: B’den başlayıp çemberi önce D, sonra C noktasında kesiyor.
- Dolayısıyla sekans parçaları BD ve B’den C’ye kadar olan tam mesafe BC.
Bu yüzden sekans parçalarının çarpımı:
4. Problemin Çözüme Uygulanması
4.1. Doğrulama: m(BAD) = m(ACD) Olduğunda Neler Olur?
- m(BAD) = α: Bu açı, B noktasından A doğrusu ile D doğrusu arasında kalan açıdır.
- m(ACD) = α: C noktasında, A doğrusu ile D doğrusu arasındaki açıdır.
- İki açı eşitse, “teğet-kiriş teoremi” veya “alternatif açı” kuralı gereği, AB’nin, A, C, D noktalarını içeren çembere teğet olduğu sonucuna varılır.
Bu çember, A, C, D noktalarından geçen tek çemberdir. B noktası bu çemberin dışında kalır. AB çizgisi çembere A noktasında değmektedir (teğet).
4.2. Teğet-Sekans Formülünü Uygula
Bu tespitten sonra, B noktasından çembere iki hat çizilir:
- Teğet:
AB - Sekans:
BDC(çemberi D ve C noktalarında keser)
Power of a point (güç merkezi) teoremine göre elde ederiz ki:
Veriler:
- BD = 4 br
- BC = BD + DC = 4 + 5 = 9 br
Dolayısıyla:
Bu da aradığımız x değeridir.
Dolayısıyla, x = 6 br.
Örnek Benzerlik ve Teğet-Kiriş Açıklamaları
Bu tarz problemsel durum “Benzerlik” konusuna da kolayca çekilebilir. Şöyle ki:
- Aynı Açılar: Angle(BAD) = Angle(ACD) varsayımı, (BAD) ile (ACD) açılarını “teğet-kiriş” koşulu altında eşitler.
- Üçgenlerde Benzerlik: Teğet-kiriş sayesinde,
ABDveACDüçgenleri arasında darbeli bir benzerlik aranabilir. Fakat en net çözümü teğet-sekans yaklaşımı sağlar. - Sonuç: “Power of a Point” teoreminin direkt kullanımı, x’in 6 olduğunu tek adımda verir.
Kavramsal Açıklamalar
Aşağıdaki tabloda, çözümde kullanılan bazı temel geometri kavramlarını özetledik:
| Kavram | Tanım | Bu Problemdeki Rolü |
|---|---|---|
| Teğet (Tangent) | Düzlemin bir çemberle tam olarak bir ortak noktaya sahip olan doğru. Burada AB, A noktasında (A, C, D’yi içeren) çembere teğettir. | ∠BAD = ∠ACD koşulunu sağladığından, AB çembere teğet. |
| Sekans (Secant) | Dışarıdaki bir noktadan başlayıp çemberi iki noktada kesen doğru. Burada BC doğrusu (B’den başlayıp D ve C noktalarında çembere değdiği varsayılır) bir sekans davranışı gösterir. | B noktasından çembere giren ve iki kesim noktası (D ve C) sağlayan doğru. |
| Güç Merkezi (Power of a Point) | Bir düzlemde dışarıdaki bir noktanın çembere göre “kuvveti (gücü)” o noktadan çizilen teğetlerin uzunluklarının karesine veya sekans parçalarının çarpımlarına eşittir. “Teğet-sekans” özel durumunda, teğet uzunluğunun karesi sekans parçalarının çarpımına eşittir. | Bu problemde, AB² = BD · BC ilişkisinden yararlanarak x’i bulmamızı sağlar. |
| Açı Eşitliği (∠BAD = ∠ACD) | İki açının eşit olması, genellikle bir çembere teğetlik veya spiral benzerlik v.b. geometrik özellikler doğurur. | Soruda verilen temel şarttır. Kaynak olarak “teğet-kiriş açı teoremi” kullanılır ve AB’nin teğet olduğu sonucuna varılır. |
| BD ve DC | BC kenarının alt bölümleridir (BD=4, DC=5). Dolayısıyla BC=9. | Sekansın iki parçası (4 ve 9) çarpılarak AB² = 36 elde edilir. |
Adım Adım Yöntemin Detaylı İncelenmesi
Burada çözümü biraz daha “adım adım” ve ders kitabı formatında gösteriyoruz:
Adım 1 – Verilenleri ve Şekli Yorumlama
- ABC üçgeninde, nokta D, BC kenarı üzerinde yer alıyor. B ile D arası 4 br, D ile C arası 5 br.
- ∠BAD = α, ∠ACD = α. Bu, B’den A’ya uzanan doğruyla, A’dan D’ye uzanan doğrunun oluşturduğu açının, C’den A’ya uzanan doğruyla, A’dan D’ye uzanan doğrunun oluşturduğu açıya eşit olduğunu söyler.
Adım 2 – Açı Eşitliğinin Yorumu
- Bir çemberde kiriş AC’nin oluşturduğu çevre açısı eğer A’da teğetle oluşan açıya eşitse, bu A noktasının teğet noktası olduğunu ispatlar.
- Diğer bir açıdan bakıldığında, “∠BAD = ∠ACD” ifadesi, “AB doğrusu, A noktasında çembere teğettir” demenin geometrik karşılığıdır.
Adım 3 – BC Doğrusunun Sekans Oluşturması
- Şekilde, B’den çıkan BD ve DC parçaları, A, C, D’yi içeren çembere “iki kesiş noktasından” giriş-çıkış yapma özelliğindedir.
- Yani BC doğrusu bu çembere bir sekans (ya da kesen) olur.
Adım 4 – Güç Merkezi Teoremi Uygulaması
- Teğet (AB) uzunluğu = x (aranan değer).
- Sekans parçası 1: BD = 4
- Sekans parçası 2: BC = BD + DC = 4 + 5 = 9
Teorem yardımıyla:
Adım 5 – Son Hesaplamalar
Bundan dolayı:
Soruda Geçen Olası Alternatif Yaklaşımlar ve İlgili Bilgiler
Her ne kadar en hızlı yol teğet-kiriş açısı teoremine başvurmak olsa da, benzerlik veya trigonometri ile de sonuca ulaşılabilir:
-
Benzerlik Yaklaşımı
- ∠BAD = ∠ACD
- Bir şekilde ∠ABD = ∠ADC da ispatlanırsa, üçgen ABD ve üçgen ADC benzer olur. Oradan da yan uzunluk oranları yazılıp çözülebilir:
$$\frac{AB}{AD} = \frac{BD}{DC} = \frac{ABD’deki\ açı}{ADC’deki\ açı}$$ - Ancak bu yol daha uzun trigonometri veya açı ispatları gerektirir.
-
Trigonometri – Sinüs Kanunu
- Üçgen ABD ve ACD incelemesinde, sinüs kanunu devreye sokulabilir.
- ∠BAD = ∠ACD = α verisini kullanarak, \sin(\alpha) üzerinden çeşitli bağıntılar türetilebilir.
- Yine sonuç en nihayetinde AB = 6 br çıkacaktır.
-
Ters Mantık Yürütme (Startejik Tahmin)
- BD = 4, DC = 5 => BC = 9.
- Seçenekler: 4, 5, 6, 8, 9.
- Basitçe “Power of a Point” bilgisine aşina olan öğrenciler, seçeneği 6 olarak test ederek 6^2 = 36 ve 4·9 = 36 ile doğrulamayı süratle yapabilirler.
Uzunluk ve Açıların Tablosu
Sorunun verilerini, cevabı ve ilgili açıları bir tabloda toplayalım:
| Eleman | Değer / İfade | Açıklama |
|---|---|---|
| BD | 4 br | BC kenarının B ile D arasındaki bölümü |
| DC | 5 br | BC kenarının D ile C arasındaki bölümü |
| BC | 9 br (4 + 5) | Üçgenin BC kenarı toplam uzunluğu |
| AB | x br | Aradığımız değer |
| m(BAD) | α | Teğet-kiriş açısını oluşturan temel koşul |
| m(ACD) | α | Teğet-kiriş açısını oluşturan temel koşul |
| (AB)^2 | BD · BC = 4 × 9 = 36 | “Power of a Point” |
| AB | 6 br | Sonuç (x = 6) |
Daha Fazla Bilgi: Teğet-Kiriş Açı Teoremi
Bu teorem aynı zamanda Alternatif Açı Teoremi olarak da bilinir ve şu şekilde ifade edilebilir:
Bir çemberdeki kirişle, o kirişin üzerindeki bir noktada teğetle yapılan açı, kirişin aynı tarafındaki çevre açısına eşittir.
Burada kirişimiz CD, çevre açısı ∠ACD, teğet noktası ise “A” oluyor. B noktası çemberin dışındadır. “Teğet” de AB doğrusudur.
İspatın Kısa Özeti
- Çemberimize (A, C, D) noktalarını yerleştiririz. A noktasında çembere çizilen teğet AB.
- AB, çembere dokunuyorsa ∠BAD açısı, çember üzerindeki karşılık gelen kiriş CD’nin gördüğü çevre açısı olan ∠ACD’ye eşit çıkar.
- Dış noktada (B), teğet çizgisinin boyu (AB) ile sekansın çarpımı (BD ve BC) arasındaki ilişki, “güç merkezi” teoremini verir: AB² = BD·BC.
Böylece sorumuzun tüm bileşenleri birbiriyle örtüşür.
Son Aşamaların Tekrarı ve Kısa Özet
- Soruda: BD = 4 br, DC = 5 br → BC = 9 br; ∠BAD = ∠ACD = α.
- Teorem: Bu açı eşitliği, A noktasında çemberle teğetlik demektir.
- Uygulama: Power of a Point → AB² = BD × BC = 4 × 9 = 36.
- Çözüm: AB = √36 = 6.
Dolayısıyla x = 6 br.
Son Söz
Bu tarz sorularda, “verilen açıların eşitliği” ipucu hemen “teğet-kiriş açısı” bağlantısını çağrıştırır: “∠BAD = ∠ACD → AB, A noktasında çembere teğettir.” Ardından “teğet-sekans çarpımı = teğet uzunluğunun karesi” formülü ile hızla x = 6 bulunur.
Cevap: 6 br.