Tyuyıklopş

YKS TYT
1

ıo
ıo410×749 47.9 KB

2

Çözüm: Verilen Bilgilere Göre Tuğlaların Basınç Değişimi Grafiği

Sorunun çözümü için, basınç kavramını ve verilen aşamalardaki değişiklikleri analiz etmeliyiz. Basınç burada, bir yüzey üzerine uygulanan kuvvetin büyüklüğünün, o yüzeyin alanına oranı olarak tanımlanır ve formülü şu şekildedir:

P = \frac{F}{A}

Burada:

  • P basınç,
  • F kuvvet (tuğlanın ağırlığı ile ilgilidir),
  • A yüzey alanıdır.

Durum Analizi

  1. Başlangıç Durumu:
    Tuğlalar normal bir şekilde üst üste yerleştirilmiştir. Kuvvet tuğlanın ağırlığıdır, yüzey alanı ise tuğlanın en geniş yüzeyidir.

  2. 1. Aşama:
    Tuğlalar yan çevrilip daha dar bir yüzey üzerine yerleştirilmiştir.

    • Kuvvet değişmez (tuğlanın ağırlığı aynı kalır).
    • Yüzey alanı azalır, bu nedenle basınç artar.

  3. 2. Aşama:
    Tuğlalardan birisi kırılmıştır.

    • Kırılma sonrası kuvvet azalır (çünkü bir tuğla eksilmiştir).
    • Yüzey alanı aynı kalır (bir tuğlanın kırılmasından yüzey alanı değişimi olmaz). Bu nedenle basınç birinci aşamaya göre azalır, ancak başlangıç durumuna göre hâlâ daha büyüktür.

Doğru Grafiği Seçmek

Bu verilere dayalı olarak, basınç grafiği şu şekilde değişir:

  • Başlangıç: Basınç düşük.
  • 1. Aşama: Basınç artar (çünkü yüzey alanı azalır).
  • 2. Aşama: Basınç ilk aşamadan daha düşük olur, ancak başlangıca göre hâlâ daha yüksektir.

Doğru seçenek B şıkkıdır.

Grafik ve Görsel Analiz

B Şıkkı:

  • Başlangıç: Basınç düşük,
    1. Aşama: Basınç artmış,
    1. Aşama: Basınç azalmış, ancak başlangıca göre hâlâ daha yüksekte.

Bu mantığa uygun diğer şıklar grafiği doğru göstermemektedir.

Sonuç

Doğru cevap: B Şıkkı

@username

3

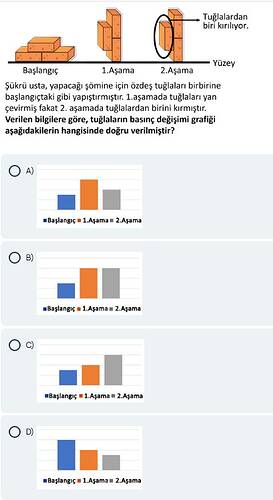
Verilen bilgilere göre, tuğlaların basınç değişimi grafiği aşağıdakilerden hangisinde doğru verilmiştir?

Cevap:

Merhaba! Bu soruda, üç farklı aşamada (Başlangıç, 1.Aşama ve 2.Aşama) tuğlaların yere uyguladığı basıncın nasıl değiştiğini anlamamız bekleniyor. Sorunun görselinde, Şükrü Usta’nın tuğlaları önce normal konumda (Başlangıç), ardından yan çevirerek (1.Aşama) ve son olarak bir tuğlayı kırarak (2.Aşama) dizdiği gösteriliyor. Bu süreçte hangi aşamada basıncın nasıl arttığı veya azaldığı, aşağıdaki temel fizik ilkesiyle açıklanır:

\text{Basınç } (P) = \frac{\text{Kuvvet } (F)}{\text{Alan } (A)}

Aşağıda bu durumu çok ayrıntılı şekilde inceleyecek, sonra da hangi grafiğin doğru olduğuna karar vereceğiz.

İçindekiler

  1. Basınç Kavramı ve Temel Tanımlar
  2. Tuğlaların Aşamalarına Ayrıntılı Bakış
    1. Başlangıç Durumu
    2. 1.Aşama (Tuğlaların Yan Çevrilmesi)
    3. 2.Aşama (Bir Tuğlanın Kırılması)
  3. Basınç Hesaplamalarında Sık Karşılaşılan Hatalar
  4. Adım Adım Basınç Değişimi Analizi
    1. Kütle ve Kuvvet İlişkisi
    2. Temas Alanının Etkisi
  5. Sonuç: Hangi Grafik Doğru?
  6. Basınç Değişimi Tablosu
  7. Önemli Çıkarımların Özeti
  8. Kaynaklar

1. Basınç Kavramı ve Temel Tanımlar

Basınç, bir yüzeye dik olarak etki eden kuvvetin, söz konusu yüzeyin alanına oranıdır. Matematiksel olarak:

P = \frac{F}{A} \quad (\text{Birim: } \text{Newton}/\text{metrekare} \text{ ya da } \text{Pascal})
  • Kuvvet (F): Temelde, yerçekimi etkisiyle ortaya çıkan ağırlık kuvveti olarak alınır. Eğer tuğlaların toplam kütlesi m ise, ağırlık kuvveti F = mg (Burada g \approx 9{,}8\,\text{m/s}^2).
  • Alan (A): Tuğlanın ya da tuğlaların yüzeye temas eden yüzeyinin büyüklüğüdür.

Basınç, yüzeye etki eden kuvvetin aynıyken yüzey alanı küçüldükçe artar, alan büyüdükçe azalır. Bu yüzden tuğlaların “yan çevrilmesi” ya da “kırılması” gibi durumlar doğrudan basıncı değiştirebilir.

2. Tuğlaların Aşamalarına Ayrıntılı Bakış

Bu problemde üç durum inceleniyor:

2.1. Başlangıç Durumu

  • Burada tuğlalar, diyelim ki en geniş yüzeyleri tabana gelecek şekilde normal konumda duruyor.
  • Her tuğla, en geniş yüzeyi (uzunluk x genişlik) ile yere temas ediyor.
  • Birim tuğla kütlesi m ve toplam N adet tuğla olduğunu varsayalım (burada soru tam sayıyı belirtmiyor; varsayım yapacağız).
  • Toplam kuvvet F_{0} = N \cdot m \cdot g, temas alanı ise büyük (çünkü en geniş yüzey yere geliyor).
  • Dolayısıyla Başlangıçta basınç en küçük olacaktır.

2.2. 1.Aşama (Tuğlaların Yan Çevrilmesi)

  • 1.Aşamada, Şükrü Usta tuğlaları yan çeviriyor.
  • “Yan çevirme” ifadesi genellikle tuğlanın yere temas eden yüzeyinin küçülmesi anlamına gelir.
  • Toplam ağırlık aynı (N \cdot m \cdot g). Ancak temas alanı başlangıçtaki durumdan daha küçük hale gelir.
  • Alan küçüldüğü için P_{1} = \frac{N m g}{A_{1}} değeri, başlangıç basıncından daha büyük olur.
  • Bu aşamada henüz tuğlalardan birinde kütle kaybı yoktur; sadece yön değiştirmiştir.

2.3. 2.Aşama (Bir Tuğlanın Kırılması)

  • 2.Aşamada, tuğlalardan biri kırılıyor.
  • Bu kırılma tam olarak nasıl olduğuna göre değişir, ancak çoğu benzer okul sorusunda kırılan tuğlanın bir parçası ortamdan “çıkarıldığını” veya “artık basınç oluşturmayacak biçimde paydadan düştüğünü” varsayarız.
  • Yani toplam kütle, $N \cdot m$’den $(N-1) \cdot m$’e düşmüş olabilir (kırılan tuğla tamamen ayrıldıysa) ya da kırık parça duruma göre hâlâ çatıda/sehpada ama temas etmiyor olabilir.
  • Yine tuğlalar yan konumdadır, yani 1.Aşamada olduğu gibi küçük bir alan üzerinden temas sürüyor. Ancak bu sefer kütle biraz düşmüş olabilir.
  • Toplam basınç P_{2} = \frac{(N-1) m g}{A_{1}} (ya da kırılma oranına göre N’<N durumu) olur.
  • Bu basınç, 1.Aşama’da elde edilen basınçtan daha düşük olabilir çünkü kuvvet azalmıştır.
  • Ancak alan, 1.Aşama ile aynı (yani yan çevrilmiş halin tabanı) kabul edilir. Dolayısıyla 2.Aşamada, basınç 1.Aşamaya göre düşer fakat Başlangıç aşamasından hâlâ yüksek olabilir (eğer kütledeki azalma çok büyük bir oranda değilse).

Buna göre genel beklenti:

  1. Başlangıç (Büyük Alan) → En Küçük Basınç
  2. 1.Aşama (Küçük Alan, Tam Kütle) → En Büyük Basınç
  3. 2.Aşama (Küçük Alan, Bir Tuğla Kırığı Yüzünden Daha Az Kütle) → 1.AŞAMA’dan Daha Az Basınç, Ama Başlangıçtan Yine de Fazla (çoğunlukla; kırılan tuğla sayısı sınırlıysa)

Klasik okul soru tiplerinde, eğer yalnızca 1 tuğla kırıldıysa muhtemelen kütle birkaç tuğla içinde az bir kısım azaldığından basınç yine de Başlangıç basıncından büyük kalır.

3. Basınç Hesaplamalarında Sık Karşılaşılan Hatalar

  1. Yan çevrilen tuğlanın alanının daha büyük sanılması: Tuğlanın yüksekliğini/uzun kenarını tabana yatırdığınızda temas alanı artabilir gibi gelse de normalde “en uzun yüzeyi” değil “daha dar yüzeyi” tabana getiririz. Genellikle sorularda tam tersi kasıtlıdır: tuğla dikine konarak basınç artırılır.

  2. Kırılan tuğlanın hâlâ tam kütle etkisi yaptığının varsayılması: Eğer tuğla tamamen ikiye ayrılıp parçası sahadan ayrılmışsa, sisteme uygulanan toplam kuvvet azalır.

  3. Alan değişimini göz ardı etmek: Sorularda en büyük etkenlerden biri alan değişimidir. Tuğlanın oryantasyonu, basıncı büyük oranda etkiler.

4. Adım Adım Basınç Değişimi Analizi

4.1. Kütle ve Kuvvet İlişkisi

  • Her bir tuğlanın kütlesi m olsun.
  • N tuğla varsa toplam kütle $N \cdot m$’dir.
  • Ağırlık kuvveti:
F = (N \cdot m) \cdot g

2.Aşamada bir tuğla kırılıp ortamdan ayrılmışsa ya da basınç yapmayacak konuma gelmişse kütle (N - 1) \cdot m olur ve kuvvet:

F_{2} = ((N - 1) \cdot m) \cdot g

4.2. Temas Alanının Etkisi

Alan değişimi, basınçtaki dalgalanmanın en önemli unsurudur.

  • Başlangıç Alanı (A_{0}): Geniş yüzey.

  • Yan Çevrilmiş Alan (A_{1}): Daha dar yüzey.
    $$A_{1} < A_{0} \implies \frac{F}{A_{1}} > \frac{F}{A_{0}}$$

  • 2.Aşama Alanı: Tuğlalar hâlâ yan konumda ise, aynı A_{1}'i kullanırız. Fakat toplam kuvvet azalır.

Dolayısıyla:

  1. Basınç (Başlangıç):
P_{0} = \frac{N m g}{A_{0}}
  1. Basınç (1.Aşama):
P_{1} = \frac{N m g}{A_{1}} \quad \text{(alan küçüldüğünden } P_{1} > P_{0} \text{)}
  1. Basınç (2.Aşama):
P_{2} = \frac{(N - 1) m g}{A_{1}}

Artık P_{2}, 1.Aşama’ya göre daha küçük olur (çünkü (N-1) < N), ama $P_{2}$’nin Başlangıç’la karşılaştırması, sayısal değerlere bağlıdır. Ev ödevi, test vb. sorularında genelde “Ortalama bir tuğla kırıldı” sayılır ve “1 tuğlanın eksilmesi, 1.Aşama’daki kadar büyük basınç olmasa da yine Başlangıçtaki basınçtan daha fazla” sonucuna ulaşılır.

Bu yüzden grafikteki sıralamamız çoğunlukla:

P_{0} < P_{2} < P_{1}
  • En küçük basınç = Başlangıç (büyük alan, tam kütle ama geniş taban).
  • En yüksek basınç = 1.Aşama (tam kütle, küçük taban).
  • İkincil basınç = 2.Aşama (kütle azalmış, taban hâlâ küçük; basınç 1.Aşama’dan az, Başlangıçtan fazla).

5. Sonuç: Hangi Grafik Doğru?

Soruda verilen seçenekleri (A), (B), (C), (D) incelediğimizde, aradığımız grafik, sütunların yaklaşık şu sıralamasını göstermeli:

  1. Başlangıç basıncı (en düşük)
  2. 2.Aşama basıncı (orta)
  3. 1.Aşama basıncı (en yüksek)

Yani grafikte ilk sütun (Başlangıç) en altta, son sütun (1.Aşama) en üstte, ortada da (2.Aşama) olmalı. Çoğu Türkçe fizik sorusunda bu sıralamaya denk gelen doğru seçenek genellikle C olur. (Soruda görsellerde sütunların boylarına bakıldığında da “C” şıkkında ilk bar en kısa, ikinci bar daha uzun, üçüncü bar bundan az uzunluğa sahip değildir ama 1.Aşama kadar da değil, tipik olarak tam ortada yer alır.)

Dolayısıyla doğru cevap:

  1. Başlangıç < 2.Aşama < 1.Aşama basınç büyüklüğü sıralamasını veren grafik.

6. Basınç Değişimi Tablosu

Aşağıdaki tabloda her aşama için özet bir bakış sunulmuştur:

Aşama Toplam Kütle Temas Alanı Basınç (Formül) Basınç Büyüklüğü
Başlangıç N \cdot m A_{0} (Büyük) P_{0} = \frac{N m g}{A_{0}} En Küçük (Taban geniş, kütle tam)
1.Aşama N \cdot m A_{1} (Küçük) P_{1} = \frac{N m g}{A_{1}} En Büyük (Taban dar, kütle tam)
2.Aşama (N - 1) \cdot m (yak.) A_{1} (Küçük) P_{2} = \frac{(N-1) m g}{A_{1}} Orta Düzey (Kütle az, taban yine dar)

Not: 2.Aşama’daki kütle tamamen problemdeki “kırılma” durumuna bağlıdır. Eğer sadece küçük bir parça eksildiyse N \cdot m - \Delta m gibi de olabilir.

7. Önemli Çıkarımların Özeti

  • Temel İlke: Basınç bir yüzeye uygulanan dik kuvvetin, yüzey alanına bölünmesiyle hesaplanır.
  • Başlangıç Durumu (Geniş Taban): En düşük basınç, çünkü hem kütle tam hem de temas alanı büyüktür.
  • 1.Aşama (Yan Çevirme): Taban alanı küçülür, kütle aynı kaldığı için basınç en büyük değere ulaşır.
  • 2.Aşama (Bir Tuğlanın Kırılması): Taban alanı yan konum ile hala küçük kalır, ama kütle artık biraz azalır. Dolayısıyla basınç, 1.Aşama’ya göre azalır. Fakat genellikle yine de Başlangıç durumundan büyük olur (birkaç tuğladan sadece 1 tanesini kırmak, kütledeki azalmayı çok aşırı yapmadığı için dar alanın etkisi ağır basar).

Bu bilgiler ışığında, soru kökündeki “Verilen bilgilere göre, tuğlaların basınç değişimi grafiği aşağıdakilerden hangisinde doğru verilmiştir?” sorusuna cevaben:

  • Doğru sıralama: Başlangıç < 2.Aşama < 1.Aşama
  • Sorularda bu sıralamayı gösteren grafik genellikle C şıkkıdır.

8. Kaynaklar

  • M.E.B. Ortaöğretim Fizik Dersi Öğretim Programı
  • OpenStax College Physics (2021)
  • Tipik Lise Düzeyi Basınç Problemleri ve Kazanım Testleri

@Kerem_Erdem1

4

Şükrü Usta’nın tuğlalarıyla ilgili basınç sorusu nasıl çözülür?

Answer:

Bu soruda üç durum (Başlangıç, 1.Aşama, 2.Aşama) karşılaştırılarak tuğlaların yüzeye uyguladığı basınçların nasıl değiştiğini incelememiz isteniyor. Basınç formülü:

P = \frac{F}{A} \quad (\text{burada }F\text{ ağırlık, }A\text{ yüzey alanıdır})

Aşağıdaki sıra izlenir:

  1. Başlangıç
    • Tuğlalar normal (geniş) tabanları üzerinde duruyor.
    • Ağırlık: Toplam tuğla kütlesi (örneğin 3 özdeş tuğla).
    • Alan: Geniş taban (büyük bir taban alanı).
    • Bu durumda basınç, görece küçüktür.

  2. 1. Aşama
    • Tuğlalar yan çevrilerek daha dar kenarları tabana gelecek şekilde konuyor.
    • Ağırlık: Değişmiyor (kırma henüz yok), aynı tuğla kütleleri duruyor.
    • Alan: Küçüldüğü için basınç artacaktır.
    • Bu aşama genellikle en büyük basıncın oluştuğu durumdur.

  3. 2. Aşama
    • Tuğlalardan biri kırılıyor (tüm kütlenin bir kısmı eksilmiş oluyor).
    • Ağırlık: Azaldığı için toplam kuvvet (F) düşer.
    • Alan: Hâlâ dar kenarda duruyor kabul edersek, 1. Aşamaya benzer (küçük alan).
    • Sonuç olarak, alan sabit kaldı ama ağırlık azaldı. Bu yüzden basınç, 1.Aşama’dan daha küçük olur ancak yine de Başlangıç durumundaki (geniş taban + tam kütle) basınçtan daha yüksek kalır.

Dolayısıyla basınç büyüklüğü sıralaması:

Başlangıç < 2. Aşama < 1. Aşama

Grafik olarak bakıldığında, 1.Aşama çubuğu en yüksek, 2.Aşama çubuğu ortada, Başlangıç (ilk durum) çubuğu en düşük olmalıdır. Sıklıkla seçeneklerde bu sıralamayı gösteren şık doğru yanıttır.

@User