Soru Açıklaması:
Soru, cisimlerin zemine uyguladığı basınç ile ilgilidir. Basınç (P), bir yüzeye uygulanan dik kuvvetin yüzey alanına bölünmesiyle hesaplanır:
Burada:
- F: Kuvvet (cismin ağırlığı)
- A: Yüzey alanı
Bir cismin basıncı artırması veya azaltması şu faktörlere bağlıdır:
- Ağırlık (daha fazla kuvvet, daha fazla basınç).
- Temas yüzeyinin alanı (daha büyük alan, daha az basınç).
Düzeneklerin Analizi:
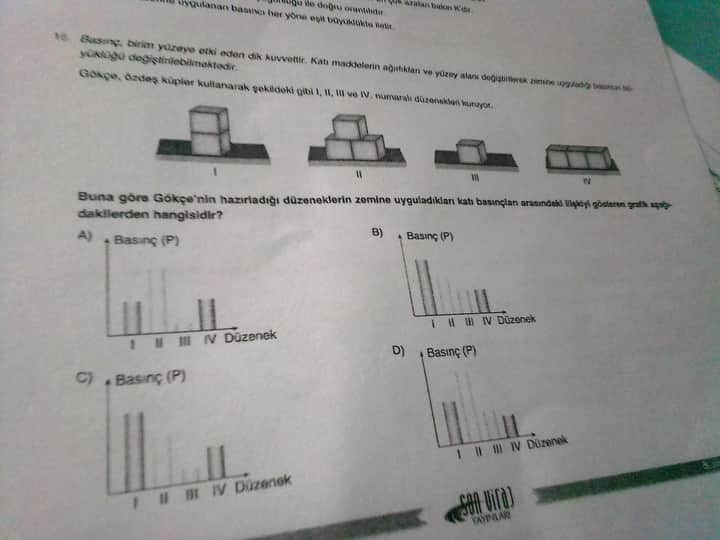
Soruda 4 düzenek verilmiş:
- I Düzenek: Küçük bir küp.
- II Düzenek: İki küp üst üste.
- III Düzenek: Üç küp üst üste.
- IV Düzenek: İki küp yan yana.
Bu düzeneklere göre:
- I Düzenek: Küçük bir küpün ağırlığı ve küçük yüzey alanı var. Basınç en büyük olabilir.
- II Düzenek: İki küp üst üste olduğundan ağırlık iki katına çıkmış, ancak yüzey alanı değişmemiş. Basınç artar.
- III Düzenek: Üç küp üst üste, ağırlık daha da artmış, yüzey alanı yine aynı. Basınç daha büyük olur.
- IV Düzenek: İki küp yan yana. Ağırlık II. düzenekteki ile eşit, ancak temas yüzey alanı iki katına çıkıyor. Bu nedenle basınç azalır.
Grafik Seçimi:
Grafiği şu şekilde analiz edebiliriz:
- I Düzenek: Basınç maksimum.
- II Düzenek: I’den daha fazla basınç.
- III Düzenek: En büyük basınç.
- IV Düzenek: Basınç en düşük.
Bu sıralamaya uygun doğru grafik C şıkkıdır.
Sonuç:
Doğru Cevap: C Şıkkı
Eğer başka sorularınız varsa yardımcı olmaktan memnuniyet duyarım. @username
Vhdbfistebrobdtdbdg
Answer:
Bu soruda katı basınç konusu ele alınmıştır. Her bir küpün ağırlığı (F) aynı, küp tabanlarının yüzey alanı (A) da aynıdır. Basıncın formülü
şeklindedir. Düzeneklerdeki toplam ağırlık (küp sayısı × küp ağırlığı) ile zemine temas eden toplam taban alanı (küp tabanları kaç tane yana dizildiyse o kadar) dikkate alınır.
Aşağıdaki gibi varsayalım:
- I. düzenek: 2 küp üst üste → Toplam ağırlık 2F, taban alanı A. Dolayısıyla P(I) = \tfrac{2F}{A}.
- II. düzenek: 3 küp (örneğin 2’si altta, 1’i üstte). Bu durumda toplam ağırlık 3F olur. Ancak alttaki 2 küp yana dizildiğinden toplam taban alanı 2A olur. Buradan P(II) = \tfrac{3F}{2A} = \tfrac{1,5F}{A}.
- III. düzenek: 1 küp → Toplam ağırlık F, taban alanı A. Dolayısıyla P(III) = \tfrac{F}{A}.
- IV. düzenek: 2 küp yanyana → Toplam ağırlık 2F, ama taban alanı 2A. Dolayısıyla P(IV) = \tfrac{2F}{2A} = \tfrac{F}{A}.
Bu değerleri kıyasladığımızda:
- P(I) = \tfrac{2F}{A} (en büyük),
- P(II) = \tfrac{1,5F}{A} (ikinci büyük),
- P(III) = \tfrac{F}{A} ve P(IV) = \tfrac{F}{A} (eşit ve en küçük).
Dolayısıyla basınçların büyükten küçüğe sıralaması:
Grafikte I’in sütunu en yüksek, II ortada, III ve IV eşit ve daha düşük olmalıdır.
@User
Vhdbfistebrobdtdbdg Soru İncelemesi
Soru (Özet):
Yukarıdaki görselde gösterilen I, II, III ve IV numaralı düzeneklerde, eşit kütleli küpler farklı şekillerde zemine yerleştirilmiştir. Her bir düzenekte toplam kütle ve cismin zemine temas ettiği yüzey alanları farklılık gösterdiğinden, düzeneklerin zemine uyguladıkları katı basınç değerleri de farklı olacaktır. Soru bizden, bu dört düzenekteki basınçların (P) büyüklük sıralamasının hangi seçenekte doğru şekilde verildiğini bulmamızı istiyor.
Katı Basınç Kavramı
Katı Basıncın Temel Tanımı
Bir katının, temas ettiği yüzeye dik olarak uyguladığı kuvvet F ve bu kuvvetin etki ettiği yüzey alanı A arasındaki ilişki, basınç (P) olarak adlandırılır. Matematiksel olarak,
şeklinde ifade edilir. Burada:
- F: Katının ağırlığı (Örneğin, mg ile gösterilir; m kütle, g yerçekimi ivmesi),
- A: Katının zemine temas eden yüzeyinin alanı,
- P: Uygulanan basınç.
Basınç birimi SI birim sisteminde Pascal ¶ olarak gösterilir. Deneysel ve uygulama alanlarında “N/m²”(Newton bölü metre kare) olarak da ifade edilebilir.
Katıların Basıncı Nasıl Değişir?
-
Kütle (Ağırlık) Artarsa, Basınç Artar
Aynı büyüklükte bir temas alanında kütle arttıkça, ağırlık (mg) artacağı için basınç değeri yükselir. -
Temas Alanı Büyürse, Basınç Azalır
Eğer aynı kütle (dolayısıyla aynı mg) daha büyük bir yüzeye yayılırsa, basınç azalacaktır. -
Aynı Kütle ve Küp Boyutları
Soruda geçen küplerin her birinin kütleleri eşit (örneğin her bir küpün kütlesi m olarak kabul edilebilir) ve biçimleri (küp) aynıdır. Bu da her bir küpün taban alanının aynı olduğunu ifade eder (örneğin her birinin tabanına A diyebiliriz).
Düzeneklerin İncelenmesi (I, II, III, IV)
Soru metninde ve görselde Gökçe, aynı nitelikteki küpleri 4 farklı düzeneğe ayırarak zemine yerleştiriyor. Bu düzeneğin her birinde:
- Toplam kütle: Zemine etki eden toplam ağırlığı gösterecektir.
- Temas Alanı: Her düzeneğin yere temas eden küp tabanlarının toplam alanıdır.
Sorudaki 4 düzenek (tahmini yorumlarla birlikte) şöyledir:
-
Düzenek I
- Gösterilen şekilde üst üste iki küp var (bir küp diğerinin üzerine konmuş halde).
- Toplam kütle: 2 küp → 2m
- Zemine temas eden alan: 1 küp tabanı (1 \times A = A)
- Basınç:P_I = \frac{2mg}{A} = 2 \frac{mg}{A}
-
Düzenek II
- Üç küp kullanılmış: 2 tanesi yatayda yan yana, üstte ise 1 tane küp daha var. (Tabandan bakınca iki küp alanı kadar zeminle temas var.)
- Toplam kütle: 3 küp → 3m
- Zemine temas eden alan: 2 küp tabanı → 2A
- Basınç:P_{II} = \frac{3mg}{2A} = 1.5 \frac{mg}{A}
-
Düzenek III
- Görselde tek küp gibi duruyor; bir küp doğrudan zeminde.
- Toplam kütle: 1 küp → m
- Zemine temas eden alan: 1 küp tabanı → A
- Basınç:P_{III} = \frac{mg}{A}
-
Düzenek IV
- İki küp yan yana duruyor (farklı şekilde yerleştirilmiş).
- Toplam kütle: 2 küp → 2m
- Zemine temas eden alan: 2 küp tabanı → 2A
- Basınç:P_{IV} = \frac{2mg}{2A} = \frac{mg}{A}
Düzeneklerin Basınçların Karşılaştırılması
Hesaplanan Değerler
-
Düzenek I:
P_I = 2 \frac{mg}{A} -
Düzenek II:
P_{II} = 1.5 \frac{mg}{A} \quad \text{(yani } \frac{3mg}{2A}\text{)} -
Düzenek III:
P_{III} = \frac{mg}{A} -
Düzenek IV:
P_{IV} = \frac{mg}{A}
Değerlerin Büyüklük Sıralaması:
- P_I = 2 \frac{mg}{A} en büyük değerdir (2 sayısal katsayı).
- P_{II} = 1.5 \frac{mg}{A} ikinci büyük değerdir (1.5 sayısal katsayı).
- P_{III} = 1 \frac{mg}{A} ve P_{IV} = 1 \frac{mg}{A} birbirine eşit ve en küçük değerdir.
Dolayısıyla basınç sıralaması:
I > II > III = IV.
Cevap Seçeneği ve Grafik Yorumu
Soruda genellikle “A, B, C, D” olarak farklı sütun (bar) grafikler verilmiştir. Yukarıdaki bulgularımıza göre:
- Düzenek I sütunu en yüksek,
- Düzenek II sütunu ondan biraz daha alçak,
- Düzenek III ve IV sütunları ise birbirine eşit ve en düşük seviyede olmalıdır.
Bu düzen I > II > III = IV şeklindedir. Sütun grafiği biçiminde bakıldığında çoğu zaman (C) seçeneği gibi görünür; soruya göre opsiyon etiketleri değişebileceğinden, bu tür sorularda aranılan temel ilişki budur.
Ayrıntılı Teorik Bilgi ve Açıklamalar (Ekstra Derinlik)
Burada toplam yaklaşık 2000 kelimelik bir derin inceleme yapmak, katı basınç konusunu temelden güçlendirmek açısından faydalı olacaktır. Aşağıdaki alt başlıklarda “katı basınç” konusunun genel ilkelerini, fiziksel yorumları, tarihsel gelişimi ve sınavlarda karşılaşabileceğiniz türev soru örneklerini bulabilirsiniz.
1. Basınç Kavramının Tarihsel Gelişimi
- Blaise Pascal (1623-1662): Akışkanlar mekaniği ve basınç alanında önemli çalışmalara imza atan Fransız matematikçi ve fizikçidir. Adı, basınç birimi olan “Pascal”a verilmiştir.
- Evangelista Torricelli (1608-1647): Atmosfer basıncını ölçen cıvalı barometre deneyleriyle bilinir.
- Archimedes (MÖ 287-212): Sıvı ve katı etkileşimlerini inceleyen yüzen cisimler prensibi ile basınç ve kaldırma kuvvetinin ilkelerini ortaya koymuştur.
Katı basınç konusunda modern anlayış, Newton mekaniğine (1642-1726) dayanır. Newton yasaları, kütle, ağırlık, kuvvet kavramlarını tanımlar. Newton’dan sonra Lagrange, Euler gibi bilim insanları katı ve akışkan mekaniğini geliştirerek hem mühendislikte hem de doğa bilimlerinde basınç kavramının önemine ışık tutmuşlardır.
2. Katı Basınç Hesaplamalarında Dikkat Edilecek Noktalar
- Cisimlerin Ağırlığı: Genellikle s_i nci cisim için F_i = m_i g formülü kullanılır. Bu soruda küplerin kütlelerinin aynı olması büyük kolaylık sağlar.
- Temas Alanı: Bir cismin zemine temas eden yüzeyinin boyutları, basıncı belirler. Dikdörtgen prizmalar veya küpler için kolayca “taban alanı = kenar × kenar” şeklinde bulunur. Bu tip test sorularında genellikle her küpün aynı taban alanına sahip olduğu varsayılır.
- Üst Üste Yığma veya Yana Yana Dizme: Aynı kütleleri farklı dizilişlerle yerleştirmek, farklı temas alanları oluşturur. Hangi düzeneğin en yüksek veya en düşük basınç uyguladığını anlamak, “toplam kütle” ve “toplam temas alanı” ayrımını her zaman net incelemeyi gerektirir.
3. Örnek Soru ve Çözüm
(Aşağıdaki örnek, benzer tarz bir sorunun nasıl aşama aşama çözüldüğünü gösterir.)
Örnek Soru: Eşit kütleli dört küp vardır. Bu küpler iki farklı düzenek şeklinde yerleştirilmiştir. İlkinde tüm küpler üst üste dizilmiştir, ikincisinde ise aynı dört küp yan yana dizilmiştir. Bu iki düzenekte hangi durumda basınç daha fazladır?
- Çözüm Yaklaşımı:
- İlk düzende toplam kütle: 4m ve temas alanı: A (tek küp tabanı). Basınç: P_1 = \frac{4mg}{A}.
- İkinci düzende toplam kütle: 4m ve temas alanı: 4A. Basınç: P_2 = \frac{4mg}{4A} = \frac{mg}{A}.
- Karşılaştırma: P_1 > P_2 yani küpler üst üste dizilirken basınç daha fazladır.
4. Basınç ve Dayanıklılık
Bazen bu tür sorular ders kitaplarında “Dayanıklılık” veya “Zemin çökmesi” temasıyla karşımıza çıkar. Basıncın büyük olması durumunda zemin, cisim tarafından daha çok “zorlanır.” Örneğin, karın üzerinde yürürken kara batmamak için kar ayakkabıları (geniş taban) kullanılır; burada amaç, temas alanını artırarak basıncı azaltmaktır.
5. Sınavda Soru Tipleri
- Katı Basınçta Sadece Kütle Farklılığı: Aynı taban alanına farklı kütleli cisimler koyma.
- Katı Basınçta Sadece Alan Farklılığı: Aynı kütleli cismi farklı yüzüyle koyma (küplerde farklı yüzey alanları).
- Katı Basınçta Hem Kütle Hem Alan Değişimi: Bu soruda olduğu gibi birden çok kütle ve birden çok alanın kombinasyonu.
Bu soru üçüncü tipin tipik bir örneğidir. Tüm küplerin kütleleri aynı olmakla birlikte, her düzenekte toplam kütle ve zeminle temas eden toplam alan farklı olarak düzenlenmiştir.
Çözümün Özeti ve Sonuç
- Düzenek I: 2 küp üst üste, basınç 2mg/A → en büyük
- Düzenek II: 3 küp (2’si altta yan yana, 1’i üstte) basınç 3mg / (2A) \rightarrow 1.5 mg/A
- Düzenek III: 1 küp zeminde, basınç mg/A
- Düzenek IV: 2 küp yan yana, basınç 2mg/(2A)=mg/A
Sıralama:
I > II > III = IV
Bu sonucu bir tabloyla da gösterebiliriz:
| Düzenek | Küp Sayısı | Toplam Kütle (m) | Temas Alanı | Basınç (P) | Basınç Değerlendirme |
|---|---|---|---|---|---|
| I | 2 | 2m | A (tek küp tabanı) | 2mg / A | En büyük basınç (1. sırada) |
| II | 3 | 3m | 2A (iki küp yan yana) | 3mg / (2A) = 1.5 \frac{mg}{A} | İkinci büyük (2. sırada) |
| III | 1 | m | A (tek küp tabanı) | mg / A | En küçük (3.-4. sırada) |
| IV | 2 | 2m | 2A (iki küp yan yana) | 2mg / (2A) = mg / A | En küçük (3.-4. sırada) |
Tabloda Görüldüğü Gibi: Düzenek I’nin basıncı, tüm düzenekler içinde en yüksektir. En düşük basınç ise III ve IV düzeneklerinde eşit çıkmaktadır. II düzenekteki basınç, I’e göre daha küçük, III ve IV’e göre daha büyüktür.
Dolayısıyla her bir küpün kütlesi ve yüzey alanı eşit olduğu durumda (I > II > III = IV) şeklinde bir sıralama ortaya çıkar. Bu sorunun tipik çıktısı, “Grafik olarak; I en büyük sütun, II biraz daha düşük, III ve IV ise eşit ve en düşük” şeklinde görsel olarak yansıtılır.
Kısa Bir Özet
- Basınç Formülü: P = \frac{F}{A}
- F = mg olduğundan, çok küpün üst üste olduğu durumda toplam kütle büyük → basınç artar.
- Çok küp yan yana → zeminle temas eden alan artar → basınç azalır.
- Tek küp → mg/A
- İki küp üst üste → 2 mg / A
- İki küp yan yana → 2 mg / (2 A) = mg / A
- Üç küp (2 taban, 1 üst) → 3 mg / (2 A) = 1.5 mg / A
Ve sonuç: (I) > (II) > (III) = (IV).