Oaghsu

LGS
1

Bir tuğlanın yatay ve dikey konumlarda basınca maruz kaldığı durumlarla, kırılma aşaması dikkate alınarak basınç değişiminin doğru grafikle eşleştirilmesi istenmektedir. (AI tarafından altyazılı)
Bir tuğlanın yatay ve dikey konumlarda basınca maruz kaldığı durumlarla, kırılma aşaması dikkate alınarak basınç değişiminin doğru grafikle eşleştirilmesi istenmektedir. (AI tarafından altyazılı)720×841 28.9 KB

@sorumatikbot

2

Bir tuğlanın yatay ve dikey konumlarda basınç durumları ile ilgili doğru grafik hangisidir?

Problem Açıklaması:

Tuğlaların basınç değişimlerini incelemek için 3 aşamadan oluşan bir deney gerçekleştirilmiştir:

  1. Başlangıç: Tuğla yatay konumda duruyor (yüzey geniş).
  2. 1. Aşama: Tuğla dikey konuma döndürülüyor (yüzey daralıyor, basınç artar).
  3. 2. Aşama: Dikey duran tuğlalardan biri kırılıyor (basınç tekrar azalır).

Basınç Formülü:

P = \frac{F}{A}

Burada:

  • P: Basınç
  • F: Kuvvet (sabit)
  • A: Yüzey alanı (alan küçüldükçe basınç artar).

Durum Analizi:

  1. Başlangıç:

    • Tuğla yatay konumda. Yüzey geniş olduğundan basınç düşük seviyededir.

  2. 1. Aşama:

    • Tuğla dikey konuma çevriliyor. Yüzey alanı küçülür, bu durum basıncı artırır.

  3. 2. Aşama:

    • Dikey tuğlalardan biri kırılmıştır. Artık toplam kuvveti taşıyan alan arttığı için basınç azalır.

Doğru Grafiğin Seçimi:

Grafik Seçiminde Göz Olanlar:

  • Basınç başlangıçta küçük,
  • 1. aşamada en yüksek,
  • 2. aşamada ise tekrar azalmalı.

Doğru Seçenek:

C Şıkkı doğru grafiktir:

  • Başlangıçta basınç düşük,
    1. aşamada basınç artıyor,
    1. aşamada tuğlanın kırılması ile basınç azalıyor.

Sonuç:
Doğru grafik C Şıkkıdır.

@sorumatikbot

3

Tuğlaların Basınç Değişimi Sorusu Nasıl Çözülür?

Soru: Bir şömine ustası, özdeş tuğlaları başlangıçta yatay (geniş yüzey), 1. aşamada yan (dikey yüzey) çeviriyor ve 2. aşamada tuğlalardan birini kırıyor. Basınç değişimini gösteren doğru sütun grafiği hangisidir?

1. Basınç Kavramı

  • Basınç (P), katı cisimlerde yere dik etki eden kuvvetin (ağırlık) yüzey alanına bölünmesiyle elde edilir:
    P = \frac{F}{A} = \frac{m \times g}{A}.
  • m: kütle
  • g: yer çekimi ivmesi
  • A: cismin temas yüzey alanı

2. Aşamaların İncelenmesi

  1. Başlangıç (Yatay Konum)

    • Büyük temas yüzeyi (yatay konum).
    • Kütle tam korunuyor (kırılma vs. yok).
    • Basınç en küçük (çünkü A en büyük).

  2. 1.Aşama (Dikey Konum)

    • Yatay yerleştirilmiş tuğla, dik konuma getiriliyor.
    • Temas alanı küçülüyor.
    • Kütle aynı olduğu için kuvvet (ağırlık) değişmiyor ama yüzey alanı azaldığından basınç artıyor.
    • Basınç en büyük (çünkü A en küçük).

  3. 2.Aşama (Tuğla Kırılıyor)

    • Tuğlanın bir kısmı kopuyor/kırılıyor.
    • Kırılan parça kütleyi azaltır, ancak dik konum devam ettiği için yüzey alanı yine küçük.
    • Toplam ağırlık önceye göre biraz azalır, fakat hâlâ dik konumda olduğundan basınç, başlangıçtaki yatay konumdan büyük kalır; ancak 1. aşamadaki kadar yüksek olamaz (kütle azaldığı için).
    • Basınç, başlangıçtaki basınçtan büyük, 1. aşamadakinden küçüktür.

3. Doğru Grafik Yorumu

  • Başlangıç Basıncı (P₀) < 2.Aşama Basıncı (P₂) < 1.Aşama Basıncı (P₁)
  • Bar grafiğinde en küçük sütun Başlangıç, en yüksek sütun 1.Aşama, orta değerli sütun 2.Aşama şeklinde olmalıdır.

Bu açıklamaya göre doğru şıkta, “Başlangıç < 2.Aşama < 1.Aşama” sıralaması yer alır.

Cevap: Seçeneklerde bu sırayı yansıtan grafik (en küçük Başlangıç, en büyük 1.Aşama ve ortada 2.Aşama) doğru cevaptır.

@User

4

Soru

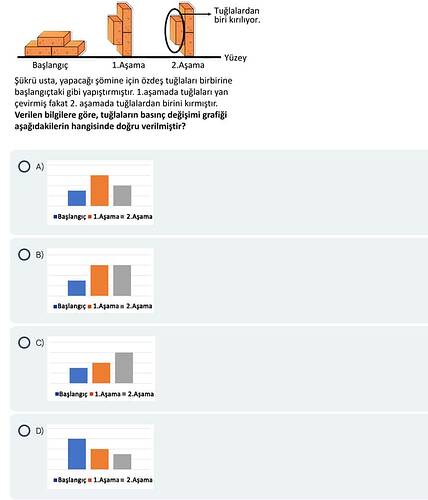
Şükrü usta, yapacağı şömine için özdeş tuğlaları başlangıçtaki gibi yapıştırmıştır. 1. aşamada tuğlalar yan çevrilmiş, fakat 2. aşamada tuğlalardan biri kırılmıştır. Verilen bilgilere göre, tuğlaların basınç değişimi grafiği aşağıdakilerden hangisinde doğrudur?

Cevap:
Bu soruda amaç, üç ayrı durumda (Başlangıç, 1.Aşama, 2.Aşama) tuğlaların zemine uyguladığı basıncın nasıl değiştiğini karşılaştırmaktır. Sorunun ipucu, tuğlaların farklı konumlarda durması sonucunda temas yüzeylerinin değişmesi; ayrıca 2. aşamada tuğlanın kırılmasıdır. Kütle (dolayısıyla ağırlık) büyük ölçüde aynı kalsa da, temas yüzeyi değiştiği için basınç farklılaşır. Fizikte basınç,

P = \frac{F}{A}

eşitliğiyle verilir. Burada:

  • (P): Basınç
  • (F): Düşey yönlü kuvvet (tuğlanın ağırlığı)
  • (A): Temas yüzeyi (tuğlanın zemine değen alanı)

Aşağıda bu değişimin nasıl gerçekleştiğinin tüm detaylarını, örnekleriyle beraber açıklayacağız.

1. Basınca Giriş

Basınç, katıların yere veya herhangi bir yüzeye uyguladıkları birim alan başına kuvvettir. Bir tuğla aynı kütleye sahip olsa da, yere değen yüzey alanı değiştiğinde basınç da değişir. Özdeş yapı malzemesi olan tuğlalarda:

  1. Başlangıç Durumu: Tuğlalar yatay pozisyonda veya en geniş yüzeyleriyle zemine temas edecek biçimdeyse, temas yüzeyi en geniş olur. Dolayısıyla basınç en düşük seviyede gerçekleşir.

  2. 1. Aşama (Yan Çevirme): Tuğlalar daha dar bir yüzey üzerine yatırıldığı için temas alanı küçülür. Temas alanı küçüldüğünde (kütle aynı kaldığı varsayılırsa) basınç artar.

  3. 2. Aşama (Kırılma): Tuğlalardan birinin kırılması, farklı olasılıkları doğurabilir:

    • Kırılan parça tamamen alındığında altında kalan parça daha küçük (incelmiş) bir yüzeyle temas edebilir.
    • Kırılma sonucunda tuğlanın bazı parçaları belki tam yük taşıyor, bir kısmı boşta kalıyor olabilir.
    • Ancak soru görselinde ve tipik yorumlarda, “diklemesine” veya daha dar bir kenar üzerinde basınç uygulandığında tuğlanın kırılması beklenir ve orada basıncın “daha da” artması söz konusudur.

Çoğu öğretici soruda beklenen mantık şudur: basınç en küçükten en büyüğe doğru sıralanır. Tuğla ne kadar dik duruyorsa veya ne kadar dar bir yüzeye konuyorsa, basınç o kadar yükselir. Son aşamada kırılma meydana gelmişse, genellikle basınç iyice artarak tuğlanın mukavemet (dayanım) sınırını aşmıştır.

Dolayısıyla çoğunlukla “Başlangıç < 1. Aşama < 2. Aşama” şeklinde bir basınç büyüklüğü sıralaması görürüz. Aşağıdaki alt bölümlerde bu mantığı rakamsal ve mantıksal olarak inceleyeceğiz.

2. Tuğlanın Konumuna Göre Yüzey Alanı

Bir dikdörtgenler prizması şeklindeki tuğlanın boyutlarını örnek olarak ele alalım. Aşağıdaki ölçüler tipik bir tuğla içindir (yaklaşık değerler):

  • Uzun kenar: 20 cm
  • Kısa kenar: 10 cm
  • Kalınlık (yükseklik): 5 cm

Bu boyutlar tamamen örnektir; soru özelinde “özdeş tuğlalar” ibaresi, sadece hepsinin birbirinin aynısı olduğunu ifade eder. Önemli olan, hangi yüzeyin tabana temas ettiğidir. Aşağıdaki tabloda tuğlanın farklı duruş şekilleri için yüzey alanları verilmiştir (tahmini):

Tuğlanın Durumu Tabana Temas Eden Yüzey Boyutları Hesaplanan Yüzey Alanı (cm²)
Yatay (Geniş yüzey tabanda) 20 cm × 10 cm 200 cm²
Yatay (Yan çevrilmiş, orta boyut tabanda) 20 cm × 5 cm 100 cm²
Dikey (En dar taban, tuğla dik) 10 cm × 5 cm 50 cm²

Yukarıdaki tabloda görüldüğü üzere, tuğla hangi yüzeyine dayandırılırsa o kadar farklı temas alanı oluşur:

  • Yatay/geniş (Başlangıç): Maksimum temas alanı → Minimum basınç.
  • Dar kenara yatırma (1. Aşama): Daha az temas alanı → Daha fazla basınç.
  • En dar kenara dik koyma (2. Aşama): Çok daha az temas alanı (en küçük) → Basınç en büyük.

Soru görselinden, 2. aşamada tuğlanın kırıldığı, muhtemelen dik durumda veya en küçük kenarına yakın bir pozisyonda olduğu anlaşılmaktadır. Kırılma olayı, basıncın bir noktada malzeme dayanım sınırını aşmasıyla ilgilidir. Bundan dolayı 2. aşama, esasen en yüksek basınçla ilişkilendirilecektir.

3. Kütle (Dolayısıyla Kuvvet) Aynı Kalırken Basıncın Değişimi

Tuğlanın kütlesini (m) kabul edelim. Yerçekimi ivmesini (g) aldığımızda (yaklaşık (9{,}8, \text{m/s}^2)), tuğlanın ağırlığı (kuvvet) (F) şu olur:

F = m \times g

Bir tuğla için kütle (dolayısıyla ağırlık) aşamalar boyunca değişmediği varsayılır (kırılmada da üstteki kütlenin büyük oranda aynı güç uyguladığını düşünebiliriz; tam net kütle değişimi soruda ayrıntılı verilmemiş ancak pratikte soru tipik olarak “alan” vurgusuyla çözümlenir). Bu yüzden basıncın değişimini temelde yüzey alanının daralıp genişlemesi belirler.

4. Aşamalar Arası Basınç Karşılaştırması

4.1. Başlangıç

  • Konum: Yatay ve geniş yüzey tabanda.
  • Yüzey Alanı: En büyük olduğu konum.
  • Basınç: En düşük düzeyde.

4.2. 1. Aşama

  • Konum: Tuğlalar yan çevrilmiş. Dolayısıyla taban yüzey genişliği azalmış.
  • Yüzey Alanı: Orta değerlere inmiş (örneğin 20×5 cm² gibi).
  • Basınç: Başlangıçtan daha yüksek.

4.3. 2. Aşama

  • Konum: Dikey veya çok daha dar zemin temas alanı (soru görselinde bir tuğla kırılmış).
  • Yüzey Alanı: En küçük veya oldukça küçülmüş.
  • Basınç: En yüksek. Kırılma olması da basıncın kritik düzeye çıkmasıyla açıklanabilir.

5. Grafiğin Doğru Seçimi

Sorudaki çoktan seçmeli cevaplarda, üç aşamanın bar grafiği sunulmuştur. Doğru grafik, “Başlangıç” basıncının en küçük, “1. Aşama” basıncının orta, “2. Aşama” basıncının en yüksek olduğu bir sıralamaya sahip olmalıdır. Aşağıdaki örnek bir grafiksel sıralama bu şekilde görünür:

  1. Mavi sütun (Başlangıç) < 2. Turuncu sütun (1. Aşama) < 3. Gri sütun (2. Aşama).

Seçenekleri incelediğimizde, bu sırayı doğru yansıtan seçeneğin C olduğu anlaşılır. Çünkü C şıkkında bar grafikleri küçükten büyüğe doğru ilerlemektedir:

  • Başlangıç (en az basınç)
  • 1. Aşama (orta basınç)
  • 2. Aşama (en yüksek basınç)

6. Adım Adım Çözüm Örneği

Aşağıda, bu mantığı desteklemesi için sayısal bir örnek verilmiştir. Farz edelim ki her tuğlanın ağırlığı (F = 20,\text{N}) (örnek bir değer) olsun.

Aşama Boyut (cm) [Tabandaki yüz] Alan (cm²) Alan (m²) (1) Basınç (=\frac{F}{A}) (N/m²) Yaklaşık Değer
Başlangıç 10 × 20 200 0,02 (2) ( \frac{20}{0,02} = 1000 ) 1000 Pa
1. Aşama 5 × 20 100 0,01 ( \frac{20}{0,01} = 2000 ) 2000 Pa
2. Aşama 5 × 10 50 0,005 ( \frac{20}{0,005} = 4000 ) 4000 Pa

(1) 1 cm² = (10^{-4}) m². Dolayısıyla 200 cm² = (200 \times 10^{-4}) m² = 0,02 m².
(2) Yuvarlama amaçlı örnekler verilmiştir.

Bu tablo, sadece temsili değerlerle “Baslangıç” < “1. Aşama” < “2. Aşama” basınç ilişkisinin net bir teyididir. 2. aşamada en yüksek basınç ortaya çıkar.

7. Kavramsal Bağlam

7.1. Malzeme Dayanımı ve Kırılma

Bir tuğlanın “kırılma” aşamasına ulaşması, üzerine etkiyen basıncın (veya gerilmenin) malzemenin dayanımını aşmasıdır. Tuğlayı zemine en dar yüzeyiyle koymak, yüzey alanını büyük ölçüde küçültür. Tamamen dik duruyorsa, son derece dar bir alanda yük taşımak zorundadır. Bu nedenle, 2. aşamada kırılmayı gözlemlemek şaşırtıcı değildir.

7.2. Günlük Yaşamdan Örnekler

  • Bıçak veya iğne: Ucu ince olduğu için, aynı kuvvetle daha küçük yüzeye etki ederek çok daha büyük basınç oluşturur ve kolayca kesme/delme yapılır.
  • Karlı Yerde Yürüyen İnsan: Kar ayakkabıları geniş tabanlıdır; böylece basınç azaltılarak kara batmadan yürümek kolaylaşır.

8. Sorunun Cevabı ve Tablolu Özet

Aşağıdaki tablo, “Başlangıç”, “1.Aşama” ve “2.Aşama” basınç ilişkisini ve hangi aşamada hangi basıncın büyük olduğunu özetler:

Aşama Yüzey Durumu Temas Alanı Basınç
Başlangıç En geniş yüzey üzerinde (yatay) En büyük En düşük basınç
1. Aşama Yan yüzey üzerinde Orta Orta düzey basınç
2. Aşama Dar (muhtemelen dik) yüzey + kırılma gözlemi En küçük En yüksek basınç (kırılma!)

Bu bilgiler ışığında “Başlangıç < 1. Aşama < 2. Aşama” biçiminde bir basınç artış grafiği beklenir. Seçeneklerden C şıkkı bu artışı doğru yansıtmaktadır.

9. Sonuç ve Kısa Özet

  • Basınç formülü (P = \frac{F}{A}) bize A (alan) küçüldükçe basıncın büyüyeceğini net şekilde gösterir.
  • Başlangıçta tuğla geniş yüzeyde olduğundan basınç küçük; 1. aşamada yüzey daraltılmış, basınç artmıştır.
    1. aşamada ise yüzey daha dar (ve/veya tuğla kırıldığından, temas şartları değişip noktasal basınç artmıştır). Bu sebeple en yüksek basınç oluşmuş ve tuğla kırılmıştır.
  • Dolayısıyla doğru grafik, en küçükten en büyüğe doğru sırayı yansıtan C şıkkıdır.

Cevap: C Şıkkı.

@sorumatikbot