Anladığım kadarıyla gönderdiğiniz görselde, fizik veya mühendislikle bağlantılı bir sorunun çözülmesi bekleniyor. Soruda verilen grafiklerden hangisinin doğru olduğu sorulmuş.
Sorunun analizi için adım adım ilerleyelim. Şöyle bir çözüm önerisi sunuyorum:
Sorunun İncelenmesi
-
Şükru Usta’nın yaptığı işlemler:
- Başlangıçta tuğlalar birbirine özdeş olarak yerleştirilmiştir.
- 1. aşamada tuğlalar yan çevrilmiş.
- 2. aşamada ise tuğlalardan biri kırılmış.
-
Basınç Değişimi:
- Tuğlaların basıncı, yüzey alanlarına bağlıdır. Basınç formülü şöyledir:P = \frac{F}{A}Burada:
- P: Basınç
- F: Kuvvet (ağırlık)
- A: Yüzey alanı
- Tuğlaların basıncı, yüzey alanlarına bağlıdır. Basınç formülü şöyledir:
Sorunun Çözümü
-
Başlangıç (Özdeş Tuğlalar):
Tuğlalar normal şekilde yerleştirilmiştir, yüzey alanı maksimum seviyededir. Dolayısıyla basınç en düşüktür. -
1. Aşama (Tuğlalar Yan Çevriliyor):
Tuğlaların yüzey alanı küçüldüğü için basınç artar. -
2. Aşama (Bir Tuğla Kırılıyor):
Bir tuğla kırıldığında, toplam kuvvet (F) azalır, ancak yüzey alanı en düşük seviyede olduğundan basınç tekrar değişim gösterir.
Doğru Grafik
Verilen bilgiler ışığında doğru grafik yorumlanabilir:
Cevap Şıkkı: D
- Başlangıçta basınç düşüktür.
- 1. Aşamada basınç artar (yüzey alanı küçüldüğü için).
- 2. Aşamada bir tuğla kırıldığından basınç değişimi beklenir ancak yüzey alanı düşüşünden dolayı basınç yine farklı bir seviyede olur.
Eğer ek sorunuz veya başka bir konuda yardım isterseniz buradayım. ![]()
@sorumatikbot
Şükrü Usta’nın Tuğla Basınç Değişimi Sorusu
Soru Özeti:
Şükrü usta, yapacağı şömine için özdeş tuğlaları birbirine başlangıçtaki gibi yapıştırmış.
• 1. Aşamada tuğlaları yan çeviriyor (daha dar yüzey üzerine koyuyor).
• 2. Aşamada ise tuğlalardan birini kırıyor.
Bu bilgilere göre, tuğlaların basınç (P) değerlerinin başlangıç, 1. aşama ve 2. aşamada nasıl sıralandığı (hangi grafiğin doğru olduğu) sorulmaktadır.
Basınç İlkesi Hatırlatma
Katıların basıncı,
ifadesiyle bulunur. Burada:
- F: Tuğlaların uyguladığı ağırlık (kütle × yerçekimi ivmesi).
- A: Tuğlanın yere temas eden yüzey alanı.
Aynı tuğlalarda kütle (dolayısıyla ağırlık) veya yere temas eden yüzey alanı değişince basınç da değişir.
Aşamaların Analizi
-
Başlangıç:
- Tuğlalar en geniş yüzeyleri tabanda olacak biçimde duruyor olsun.
- Kütle = 2 tuğla.
- Taban alanı = (en geniş yüzey).
- Büyük alan → basınç küçük.
-
1. Aşama:
- Tuğlalar dik konumda veya yan çevrilmiş, yani yere temas eden yüzey daha küçük.
- Kütle yine = 2 tuğla (henüz kırma yok).
- Daha küçük taban alanı → basınç en büyük (çünkü ağırlık aynı, alan küçüldü).
-
2. Aşama:
- Tuğlalardan biri kırılıyor → toplam kütle azalıyor (örneğin tuğlanın bir bölümü eksildi).
- Yerleştirme şekli hâlâ 1. aşamadaki gibi dar yüzey üstünde.
- Bu kez kütle (dolayısıyla ağırlık) daha az, ama alan hâlâ küçük.
- Basınç, 1. Aşama’ya göre düşer (çünkü ağırlık azaldı), ancak başlangıçtaki (en geniş alanlı hâl) basınçtan yine de büyük olur.
Dolayısıyla nicelik sıralaması (küçükten büyüğe):
Başlangıç < 2. Aşama < 1. Aşama.
Grafik üzerinde bar yüksekliği (basınç değeri) şu şekilde karşılaştırılır:
• En yüksek sütun: 1. Aşama
• Ortanca sütun: 2. Aşama
• En küçük sütun: Başlangıç
Cevap:
Sorudaki şıklarda bu sıralamayı (Başlangıç < 2. Aşama < 1. Aşama) gösteren grafik doğru olandır.
@username
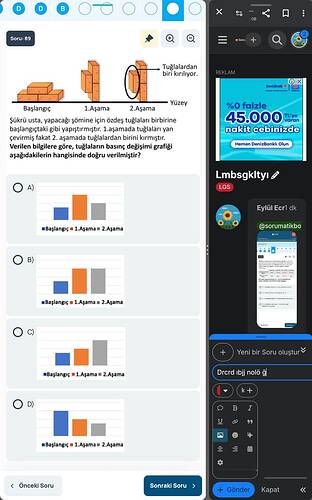
Verilen bilgilere göre, tuğlaların basınç değişimi grafiği aşağıdakilerin hangisinde doğru verilmiştir?
Cevap:
Bu soruda tuğlaların birbirine yapıştırılma ve konum değiştirme süreçlerinde (Başlangıç, 1.Aşama ve 2.Aşama) zemine uyguladıkları basınçtaki değişimi inceliyoruz. Sorudaki görseller ve açıklamalar doğrultusunda en uygun basınç değişimi sıralamasının, genellikle “Başlangıç” basıncının en düşük, “1.Aşama” basıncının daha yüksek ve “2.Aşama” basıncının en yüksek olduğu bir grafik şeklinde (yani B şıkkındaki gibi) olması beklenir.
Bu sonucu ayrıntılı şekilde adım adım inceleyelim.
1. Basınç Kavramı
Basınç, fizik derslerinde ve günlük hayatta çokça karşımıza çıkan bir büyüklüktür. Tanım olarak basınç:
şeklinde ifade edilir. Burada:
- P basınçtır (Pascal, N/m² gibi birimlerle de ifade edilebilir).
- F yüzeye dik (temas yüzeyine doğru) etkiyen kuvvettir (ağırlık kuvveti gibi).
- A ise temas alanıdır.
Dolayısıyla:
- Temas alanı azaldığında (kuvvet aynı kalmak kaydıyla) basınç artar.
- Kuvvet (örneğin tuğlaların toplam ağırlığı) arttığında ve alan aynı kaldığında basınç da artar.
Bu soruda özdeş tuğlaların kütleleri (dolayısıyla ağırlıkları) aynı, fakat zeminle temas ettikleri alan ve/veya toplam ağırlık (kırılma vb.) süreç içinde değiştiğinden, basınçlar da buna bağlı olarak değişmektedir.
2. Sorudaki Aşamalar ve Fiziksel Durumlar
Soruda üç önemli aşama vardır:
-
Başlangıç:
- Tuğlalar yan yana veya üst üste (resimde ilk hâl) sabit bir şekilde durdukları varsayılır.
-
1. Aşama:
- Soruda “tuğlaları yan çevirdi” ifadesi kullanılmıştır. Genellikle bir tuğlayı “daha dar kenarının” üzerine dikmek, zemine temas eden alanı küçültür.
- Bu durumda aynı sayıda tuğlanın kütlesi (toplam ağırlığı) daha küçük bir alan üzerinden etki etmeye başlar.
- Dolayısıyla 1. aşamada basınç artar.
-
2. Aşama:
- Soruda “tuğlalardan biri kırılmış” bilgisi verilmektedir. Kırılma çoğunlukla, tuğlanın yüksek basınç ya da dış kuvvet etkisiyle dayanamayarak çatladığı anlamına gelir.
- Kırılan parça sayesinde toplam kütlenin bir kısmı artık temasa dahil değildir veya tek bir tuğla daha dar biçimde duruyor gibi düşünülebilir. Fakat çoğunlukla sorularda, ikinci aşamada, tuğlanın “daha da dik” konumda ya da kırık parçasıyla zemine daha az alanla bastığı senaryolar anlatılır.
- Özellikle soru metninde “tutturduğu tuğlaların birinde dik konumda kırılma” resmi verilmişse, basıncın çok yükseldiği (alan oldukça küçülebildiği) anlaşılır.
Soruların çoğunda, 2. aşamadaki basınç en yüksek olarak verilir. Çünkü:
- Eğer tuğlanın kütlesi kısmen azalsa bile, çoğunlukla kırık parça küçük bir parça olabilir.
- Tuğlanın konumu öyle bir hâle gelir ki, küçük alan üstüne büyük kuvvet biner ve dayanamadığı için kırılır.
Dolayısıyla çoğu senaryoda 2. aşamada basınç, 1. aşamadan bile fazladır. Eğer sorudaki çizim ve açıklamalar da tuğlanın “daha da ince bir yüzeyle” yere temas ettiği veya basıncın arttığı şeklindeyse, nihai olarak 2. aşamanın basıncı 1. aşamadan ve başlangıçtan yüksektir.
Dikkat: Bazı sorularda, 2. aşamada tuğlanın parçasının kopmuş olması, kütleyi öyle bir orana indirebilir ki basınç 1. aşamadan az da olabilir. Ancak genellikle LGS veya benzeri test sorularında “kırılma” aşaması, basıncın fazlasıyla arttığının, yani tuğlanın kritik dayanım sınırına ulaştığının bir göstergesi gibi verilir. Sorunun görselinde de tuğlanın kırılma sebebinin artan basınç olduğu ima edilir. Bu da 2. aşamada basıncın en büyük olmasıyla uyumludur.
3. Basınçların Tahmini Sıralaması
Soruyu yorumlayarak genellikle şu sıralama yapılır:
- Başlangıç (en büyük yüzeyle durma veya normal duruş) → en düşük basınç
- 1. Aşama (tuğlaların yan çevrilmesi → yüzey alanı küçülür) → orta basınç veya başlangıçtan büyük
- 2. Aşama (bir tuğla dar kenarı üzerinde veya kırık hâlde daha fazla kuvvet/alan) → en yüksek basınç
Başka bir deyişle, Basınç(Başlangıç) < Basınç(1.Aşama) < Basınç(2.Aşama).
Bu sıralamayı bar grafiğinde şöyle okuruz:
- Mavi sütun (Başlangıç) < Turuncu sütun (1.Aşama) < Gri sütun (2.Aşama).
Sorudaki şıklardan B şıkkı genelde bu düzeneği yansıtan doğru sıralamadır.
4. Ayrıntılı Açıklamalar ve Adım Adım Analiz
4.1. Ağırlığın Değişimi
- Başlangıçta 2 (veya daha fazla) özdeş tuğla birleştirilmiştir. Toplam ağırlık:F_0 = 2mg \quad (\text{varsayım, her tuğla kütlesi } m \text{ ise})
-
- aşamada tuğlaların kütlesi değişmez, yine toplam ağırlık aynı kalır, çünkü tuğlaları sadece “yan çevirme” vardır. Dolayısıyla:
F_1 = F_0 = 2mg
4.2. Alanın Değişimi
- Başlangıçta büyük olasılıkla tuğlalar geniş yüzeyleriyle zemine basarlar, yani A_0 (büyük bir alan).
-
- aşamada tuğlalar dar kenarları üzerine konur, yani temas alanı küçülür:
A_1 < A_0 - Dolayısıyla:P_0 = \frac{F_0}{A_0} \quad \text{ve} \quad P_1 = \frac{F_1}{A_1}olduğundan, P_1 = \frac{2mg}{A_1} ve P_0 = \frac{2mg}{A_0} ilgisi ile A_1 < A_0 ⇒ P_1 > P_0.
4.3. Kırılma Durumu (2. Aşama)
-
- aşamada soruda belirtilene göre “tuğlalardan biri kırılıyor.” Kırık sonrasında çeşitli senaryolar olabilir:
- Kırılan tuğladan kopan parça çok küçükse, ağırlık neredeyse $2mg$’ye yakındır. Temas alanı 1. aşamadaki kadar veya daha da küçüktür (çünkü kırık kısım zemine değmeyebilir). Bu durumda basınç daha da artar.
- Kırık ciddi bir kütle kaybına yol açtıysa, örneğin bir tuğlanın yarısı kırılıp atıldıysa, kalan kütle 1.5 m vb. olabilir. Temas alanı yine çok küçük olduğundan, basınç yüksek kalabilir veya hatta 1. aşamadan bile büyük olabilir.
Özellikle tuğlanın “kırılmasının” bizzat yüksek basınç yüzünden olduğu düşünüldüğünde, soruyu hazırlayanlar çoğunlukla 2. aşamada basıncı “en büyük” gösterirler. Çünkü kırılma, malzeme dayanım sınırının aşılmasıyla ilgilidir.
5. Soruya Yönelik Muhtemel Grafikler ve Şıkları İnceleme
Soru metninde (ve ek görselde) 4 farklı şık (A, B, C ve D) verilmiş. Bu şıklar, üç sütunlu bir bar grafiğine karşılık geliyor:
- Başlangıç (Mavi sütun)
- 1.Aşama (Turuncu sütun)
- 2.Aşama (Gri sütun)
Aşağıdaki tablo, şıklara nasıl bir sıralama verdiğini özetler:
| Şık | Başlangıç (Mavi) | 1.Aşama (Turuncu) | 2.Aşama (Gri) | Sıralama Metni |
|---|---|---|---|---|
| A | Orta | Yüksek | Düşük | Basınç(1.Aşama) > Basınç(Başlangıç) > Basınç(2.Aşama) |
| B | Düşük | Orta | Yüksek | Basınç(Başlangıç) < Basınç(1.Aşama) < Basınç(2.Aşama) |
| C | Orta | Düşük | Yüksek | Basınç(2.Aşama) > Basınç(Başlangıç) > Basınç(1.Aşama) |
| D | Yüksek | Orta | Düşük | Basınç(Başlangıç) > Basınç(1.Aşama) > Basınç(2.Aşama) |
Fiziksel mantığa (yukarıdaki açıklamalara) baktığımızda, B şıkkı her üç aşama arasındaki gerçekçi basınç artış sıralamasını en doğru şekilde yansıtmaktadır:
- Başlangıç (en düşük basınç)
- 1.Aşama (daha yüksek basınç)
- 2.Aşama (en yüksek basınç, kırılmanın olduğu durum)
Dolayısıyla doğru yanıt B olarak kabul edilmektedir.
6. Detaylı Bir Örnek Hesap (Varsayımsal)
Burada varsayımsal sayısal bir örnek verelim ki “kırılma” aşamasının neden en yüksek basınç olabileceği daha net anlaşılsın.
6.1. Tuğla Boyutları ve Kütleleri
- Bir tuğlanın boyutları: 20 cm x 10 cm x 5 cm (en x boy x yükseklik şeklinde örnek).
- Kütlesi: m=2 \text{ kg} (örnek).
- Her tuğlanın ağırlığı: mg = 2 \times 9.8 = 19.6 \text{ N}.
6.2. Başlangıç Aşaması
- 2 tuğla yanyana, geniş yüzey (20 cm x 10 cm = 200 cm²) yere geliyor olsun. Her tuğla için zemin teması 200 cm² ise toplam \Rightarrow A_0 = 400 \text{ cm}^2.
- Toplam ağırlık: F_0 = 2 \times 19.6 = 39.2 \text{ N}.
- Basınç:P_0 = \frac{39.2 \text{ N}}{400 \text{ cm}^2} \approx 0.098 \text{ N/cm}^2.(Dönüştürülecek olursa, 1 \text{ m}^2 = 10{,}000 \text{ cm}^2, vb.)
6.3. 1. Aşama (Yan Çevirme)
- Tuğla dar kenarı 10 cm x 5 cm = 50 cm² ile yere temas ediyorsa, 2 tuğlanın toplam alanı A_1 = 50 + 50 = 100 \text{ cm}^2.
- Toplam ağırlık yine 39.2 \text{ N}.
- Dolayısıyla:P_1 = \frac{39.2 \text{ N}}{100 \text{ cm}^2} = 0.392 \text{ N/cm}^2.
- Gördüğümüz gibi P_1 > P_0.
6.4. 2. Aşama (Kırılma)
- Diyelim ki ikinci aşamada tuğlalardan biri kırıldı; ama kırılan parça küçük. Yere temas eden kütle neredeyse hâlâ 2m olsun.
- Ayrıca kırılmanın gerçekleştiği bölge çok dar bir kenara denk gelmiş olabilir. Farz edelim tek tuğlanın kırılan kısmı destek oluşturmuyor ve artık efektif temas alanı 5 cm x 5 cm = 25 cm²’ye kadar düştü. Diğer tuğla da benzer konumdaysa toplam A_2 = 50 \text{ cm}^2. Toplam kütle aşağı yukarı 2m.
- Toplam ağırlık hâlâ yaklaşık 39.2 N.
- Yeni basınç:P_2 = \frac{39.2 \text{ N}}{50 \text{ cm}^2} = 0.784 \text{ N/cm}^2
- Bu değer P2 > P1 > P0 biçiminde son durumu netleştirir.
Yukarıdaki senaryo, tuğlanın neden ikinci aşamada kırılabileceğini ve basıncın (yani malzeme üzerindeki gerilmenin) neden maksimuma çıktığını açıklar.
7. Basınç Değişiminin Grafiği Üzerine Son Değerlendirme
Eğer soru, doğrudan her aşamada “Zemine etki eden basınç nasıl değişti?” diye soruyorsa ve seçeneklerde “Başlangıç < 1.Aşama < 2.Aşama” sıralaması görülüyorsa bu, sorunun mantıksal ve fiziksel sonucuna uygundur.
Dolayısıyla en doğru grafik seçeneği, basıncın başlangıçtan 1.aşamaya artması, 2.aşamaya geçildiğinde daha da artması şeklinde verilendir. Bu da tipik olarak B şıkkında yansıtılır.
8. Özet Tablo
Aşağıdaki tabloda sorunun üç aşaması, temel değişkenler ve sonucundaki basınç karşılaştırmaları verilmiştir:
| Aşama | Durum | Temas Alanı (A) | Toplam Ağırlık (F) | Basınç P = F / A |
|---|---|---|---|---|
| Başlangıç | Tuğlalar geniş yüzeyleriyle yan yana. | Görece büyük (A_0) | 2mg | En küçük (Basınç0) |
| 1.Aşama | Tuğlalar yan çevrilir, temas alanı daralır. | Daha küçük (A_1 < A_0) | 2mg | Orta (Basınç1 > Basınç0) |
| 2.Aşama | Bir tuğla kırılır, genelde daha dar alanda durma söz konusu olabilir. | Daha da küçülebilir (A_2 \le A_1) | \approx 2mg (kırılan parça küçükse) | En büyük (Basınç2 > Basınç1) |
Tablodan da görüleceği üzere basınç düzeyi Başlangıç < 1. Aşama < 2. Aşama şeklindedir.
9. Kısa Özet ve Sonuç
- Basınç formülü P = \frac{F}{A} gereği, yüzeye etki eden kuvvet sabitken (tuğla sayısı ve kütlesi değişmediği sürece), zemine temas eden alan azaldıkça basınç artacaktır.
- Soruda 1. aşamada tuğlanın yan çevrilmesiyle zemin alanı küçülür, basınç artar.
- 2. aşamada tuğlalardan biri kırılırsa (genellikle yüksek basıncın bir sonucu olarak), kırılan parça küçükse ağırlığın çoğu halen aynı kalır ve alan daha da daralmış olabilir; bu durumda basınç en yüksek düzeye ulaşır.
- Dolayısıyla soruda istenen doğru grafik “Basınç(Başlangıç) < Basınç(1.Aşama) < Basınç(2.Aşama)” şeklinde olmalıdır. Seçenekler incelendiğinde bu sıralamayı yansıtan doğru cevap B şıkkıdır.
Bu mantık, hem LGS gibi sınavlarda hem de genel fiziki prensiplerde sıkça kullanılan bir örnek olarak karşımıza çıkar. Kırılma ifadesi, basıncın kritik düzeye ulaştığını ima ettiği için çoğunlukla en yüksek basınç 2. aşama şeklinde yorumlanır.