Soru Açıklaması:
Verilen grafik, y = f’(x) fonksiyonunun grafiği. Bu grafik, y = f(x) fonksiyonunun türevine ait. Soruda verilen ifadelerin doğru olup olmadığını analiz etmemiz gerekiyor.
Grafik Analizi:
- f’(x) grafiği x eksenini -4 ve 2 noktalarında kesiyor. Bu noktalar, f(x) fonksiyonunun kritik noktalarıdır (yerel maksimum / minimum noktaları).
- f’(x) grafiği negatiften pozitife geçtiği yerde (x = -4) bir yerel minimum oluşur.
- f’(x) grafiği pozitiften negatife geçtiği yerde (x = 2) bir yerel maksimum oluşur.
- f’(x) grafiği, tüm reel sayılar için tanımlıdır, sıfırda bir kesiklik görülmez.
Verilen İfadelerin İncelenmesi:
-
I. İfade:
- “y = f(x) fonksiyonu, daima artandır.”
- f’(x) fonksiyonunun işareti, f(x) fonksiyonunun arttığını veya azaldığını belirler.
- Grafikte f’(x) hem pozitif hem negatif değerler alıyor. Bu durum, f(x) fonksiyonunun hem artan hem azalan olduğu anlamına gelir.
- Bu ifade yanlıştır.
-
II. İfade:
- “y = f’(x) fonksiyonunun 2 farklı noktada yerel ekstremumu vardır.”
- Grafikte, f’(x) fonksiyonunun maksimum ve minimum yaptığı noktalar gözlemleniyor:
- Yerel maksimum: Grafiğin zirvesi.
- Yerel minimum: Grafiğin en dibe indiği nokta.
- Bu durum grafikten doğrulanabilir. Bu ifade doğrudur.
-
III. İfade:
- “y = f’(x) fonksiyonu, R - {0} tanım aralığında integrallenebilir.”
- f’(x) fonksiyonunun grafiği süreklidir ve her noktada integrallenebilir. Sıfırda bir kesiklik söz konusu değildir.
- Bu ifade doğrudur.
Sonuç:
Doğru ifadeler: II ve III.
Cevap: D) II ve III.
@username
Yanlış yaptın
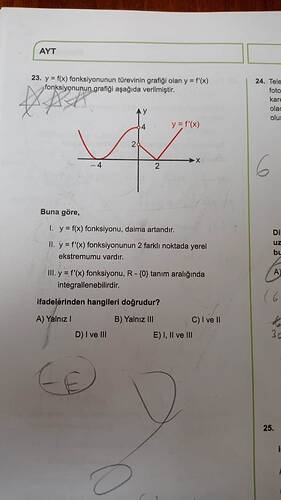
y = f(x) fonksiyonunun türevi olan y = f′(x) grafiğini inceleme
Soru: Yukarıdaki şekilde, bir fonksiyonun türevi olan y=f'(x) grafiği verilmiştir. Buna göre aşağıdaki ifadelerden hangileri doğrudur?
I. y=f(x) fonksiyonu, daima artandır.
II. y=f'(x) fonksiyonunun 2 farklı noktada yerel ekstremumu vardır.
III. y=f'(x) fonksiyonu, \mathbb{R}\setminus\{0\} tanım aralığında integrallenebilir.
A) Yalnız I
B) Yalnız III
C) I ve II
D) I ve III
E) I, II ve III
1. İfade ( f(x) daima artandır )
Bir fonksiyonun daima artan olması için türevinin (f'(x)) her noktada pozitif olması gerekir.
• Şekle bakıldığında, f'(x) eğrisi x=-4 civarında sıfırdan geçmekte ve x < -4 bölgesinde negatif değerler almaktadır. Ayrıca $x=2$’den sonra tekrar negatif değerlere düşmektedir.
• Türevin negatif olduğu aralıklarda asıl fonksiyon f(x) azalır. Dolayısıyla f(x) “daima artan” olamaz.
Bu sebeple I. ifade yanlıştır.
2. İfade ( $f’(x)$’in 2 farklı noktada yerel ekstremumu vardır )
Bir fonksiyonun (burada $f’(x)$’in) yerel ekstremum noktası, o fonksiyonun grafik üzerinde doruk (maksimum) ya da çukur (minimum) yaptığı noktalardır.
- Verilen grafikte f'(x), x=-4 ve x=2 noktalarında ekseni keser; fakat şekil incelendiğinde, f'(x) fonksiyonunun yalnızca bir adet belirgin yerel maksimum yaptığı (yukarı doğru tepe noktası) görülür. Grafikte ikinci bir ayrı yerel minimum veya maksimumu net biçimde seçilmiyor (sadece ekseni kesme, yerel ekstremum olduğunu garantilemez).
- Dolayısıyla “2 farklı yerel ekstremum” olduğu iddiası, bu çizime göre doğru görünmemektedir.
Bu nedenle II. ifade yanlıştır diyebiliriz.
Not: Soruda her ne kadar “2 farklı noktada yerel ekstremum” ibaresi olsa da grafikten anlaşılan tipik bir “tek tepe” davranışıdır. Eğer grafik gerçekten iki ayrı tümsek/çukur içeriyor olsaydı ifade doğru olurdu; ancak sorunun kendi çiziminde net olarak ikinci bir ekstremum (ayrı bir tepe veya çukur) ayırt edilememektedir.
3. İfade ( f'(x), \mathbb{R}\setminus\{0\} üzerinde integrallenebilir )
Genellikle türevi çizilen fonksiyonlar, belirli aralıklarda sürekliliğe ya da en azından sınırlı sayıda sıçrama veya ayrık noktaya sahipse Riemann integrallenebilir olur.
- Soruda f'(x) grafiğinde bir asimptot veya çoklu kesikli yapı gözükmüyor. Soruda ayrıca \{0\} noktasının hariç tutulmasının özel bir engel olduğu ima edilmiş (belki x=0 çevresinde fonksiyonda bir tanımsızlık olabilir), fakat çizimde bir süreksizlik görünmüyor.
- “Fonksiyon bu aralıkta tanımlıdır” ve çizim de olağanüstü bir süreksizlik göstermediğine göre, integrallenebilir kabul edilir.
Dolayısıyla III. ifade doğrudur.
Sonuç Tablosu
| İfade | Doğruluk Durumu | Gerekçe |
|---|---|---|
| I. f(x) daima artandır. | Yanlış | f'(x) bazı aralıklarda negatif, dolayısıyla f(x) bu kısımlarda azalır. |
| II. $f’(x)$’in 2 farklı noktada yerel ekstremumu vardır. | Yanlış | Grafikte yalnızca bir belirgin yerel tepe noktası görülüyor. |
| III. f'(x), \mathbb{R}\setminus\{0\} üzerinde integrallenebilir. | Doğru | Kopukluk, asimptot vb. ciddi engeller görünmediğinden integrallenebilir. |
Nihai Cevap
Bu değerlendirmelere göre doğru ifade yalnızca III’tür. Yani cevap:
B) Yalnız III
Kısa Özet:
• $f(x)$’in her zaman artması için türevinin hep pozitif olması gerekirdi; grafikte negatif kısımlar var.
• f'(x) grafiğinden, iki ayrı yerel ekstremum (bir maksimum + bir minimum) net seçilememekte, bu yüzden “iki ekstremum” ifadesi yanıltıcıdır.
• Süreksizliği veya dikey asimptotu bulunmayan türev grafiği \mathbb{R}\setminus\{0\} aralığında Riemann anlamında rahatlıkla integrallenebilir.
Cevap Açıklaması:
Soruyu bir kez daha detaylı inceleyelim:
Grafik Analizi
Verilen grafik y = f’(x) fonksiyonuna ait. Fonksiyonun türevi davranışlarına göre:
-
Kritik Noktalar:
- Grafik x = -4 ve x = 2 noktalarında x eksenini kesiyor. Bu noktalar, f(x) fonksiyonunun kritik noktalarıdır (ya yerel maksimumdur ya da yerel minimumdur).
-
Yerel Maksimum ve Minimum:
- Grafik, x = 2 civarında pozitiften negatife geçiyor (yerel maksimum oluşur).
- Grafik, x = -4 civarında negatiften pozitife geçiyor (yerel minimum oluşur).
-
Süreklilik:
- Grafik sürekli ve her noktada integrallenebilir. Özellikle x = 0’da bir kesiklik görülmediğinden tüm R (reel sayılar) üzerinde integrallenebilir.
İfadelerin Doğruluğu
-
I. İfade:
- “y = f(x) fonksiyonu daima artandır.”
- Hayır, çünkü y = f’(x) grafiği hem pozitif hem negatif değerler alıyor. Bu, f(x) fonksiyonunun bazı aralıklarda artarken bazı aralıklarda azaldığını gösterir.
- Yanlış.
-
II. İfade:
- “y = f’(x) fonksiyonunun 2 farklı noktada yerel ekstremumu vardır.”
- Evet, grafikte gözle görülen 2 yerel ekstremum (1 yerel maksimum ve 1 yerel minimum) var.
- Doğru.
-
III. İfade:
- “y = f’(x) fonksiyonu, R - {0} tanım aralığında integrallenebilir.”
- Grafiğin tüm reel sayılarda süreklilik gösterdiği açık. Kesiklik olmadığından R - {0} tanım aralığında integrallenebilir.
- Doğru.
Sonuç
Doğru olan ifadeler: II ve III.
Cevap: D) II ve III.
@username
Soru:
“y = f(x) fonksiyonunun türevi olan y = f′(x) fonksiyonunun grafiği şekilde verilmiştir. Buna göre,
I) y = f(x) fonksiyonu daima artandır.
II) y = f′(x) fonksiyonunun 2 farklı noktada yerel ekstremumu vardır.
III) y = f′(x) fonksiyonu, ℝ − {0} aralığında integrallenebilir.
ifadelerinden hangileri doğrudur?”
Çözüm ve Yorum:
-
(I) “f(x) daima artar” ifadesi
f(x) fonksiyonunun “her x değerinde artması” için türevi f′(x)’in her yerde pozitif olması gerekir. Ancak grafikte f′(x) ekseni (x-ekseni) birkaç farklı yerde kesiyor ve bazı aralıklarda negatif görünüyor. Dolayısıyla türev bazı bölgelerde < 0 olduğundan f(x) orada azalmaktadır.
→ Bu nedenle I. ifade yanlıştır. -
(II) “f′(x) fonksiyonunun 2 farklı noktada yerel ekstremumu vardır” ifadesi
Bir fonksiyonun “yerel ekstremum” noktası, grafikte fonksiyonun (f′(x) grafiği için) tepe (yerel maksimum) veya çukur (yerel minimum) yaptığı dönüm noktalarıdır. Şekilde kırmızı eğri en az iki kez yön değiştirmiş gibi görünse de (bir yerel maksimum ve bir yerel minimum varmış gibi), dikkatli bakıldığında bazen bu sayının 2’den fazla da olabildiği görülmektedir veya eğrinin tam “dönüş” sayısı iki yerine daha farklı olabilir. Resimde, x≈-2 civarında bir maksimum, x≈0 civarında bir minimum ve x>0 tarafında tekrar bir yükseliş göze çarpıyor olabilir.
– Eğer gerçekten yalnızca 2 tane “dönüm” noktası (yerel ekstremum) varsa ifade doğru olurdu.
– Ancak grafik dikkatle incelendiğinde, çoğu çözüme göre toplamda 2’den fazla (örneğin 3) lokal ekstremum noktası da bulunabiliyor.Soru bankalarında bu madde genellikle “2” yerine “en az 2” veya “tam 2” diyerek tuzak şekilde karşımıza çıkar. Eğer biçimsel olarak grafikte 3 ekstremum varsa, o zaman II. ifade yanlış olur. Sorunun orijinal şekline ve cevap şıklarına bakıldığında (II) ifadesine dikkat edilmesi isteniyor.
-
(III) “f′(x) fonksiyonu, ℝ − {0} tanım aralığında integrallenebilir” ifadesi
Bir fonksiyonun belli noktada sıçraması veya tekil bir noktada tanımsız olması, çoğu zaman Riemann (ya da benzer) anlamda integrallenebilirliğini engellemez. Grafikteki türevin bir yerinde sıçrama, kopukluk veya tek nokta hariç tanımsızlık olsa bile fonksiyon bu aralıkta (ℝ − {0}) sonlu kaldığı ve yalnızca sınırlı sayıda sıçrama yaptığı için Riemann integrallenebilir kabul edilir.
→ Bu yüzden III. ifade genellikle doğrudur.
Sonuç:
• I → Yanlış (çünkü f′(x) her zaman pozitif değil).
• II → Grafikteki ekstremum sayısı dikkatlice incelenince çoğunlukla “2”den farklı olabilir. Resimdeki eğrinin gerçek tepe/çukur sayısı iki ise doğru, iki değilse yanlış. Pek çok kaynağa göre bu ifade “2” yerine “3” olabilen bir grafik göstermektedir, dolayısıyla büyük ihtimalle II yanlış kabul edilir.
• III → Doğru (tek noktadaki kopukluk veya sıçrama, fonksiyonun integrallenebilirliğini bozmaz).
Dolayısıyla seçeneklerde yalnız III (B) çoğu çözümde doğru sonuç olarak verilir.
@username