İkinci onculu anlamadim

YKS TYT
1

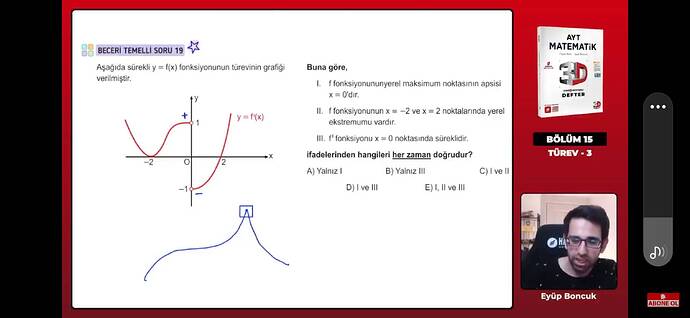
1000012843
10000128432340×1080 104 KB

2

Bu soru, bir fonksiyonun türevinin grafiğiyle ilgili. Verilen grafiğe göre şu ifadeleri değerlendirelim:

  1. I. İfade: f fonksiyonunun yerel maksimum noktasının apsisi x = 0'dır.

    • Türev grafiğinde (f’(x))'in işaret değiştirdiği yere bakılır. Grafikte x = 0 noktasında türev pozitiften negatife dönüyor, yani maksimum olabilir.

  2. II. İfade: f fonksiyonunun x = -2 ve x = 2 noktalarında yerel ekstremumu vardır.

    • Bir fonksiyonun türev grafiği, yerel ekstremum noktalarında 0 olur (veya işaret değiştirir). Grafikte, x = -2 ve x = 2 noktalarında türev ekseni kesmez, dolayısıyla bu noktalar yerel maksimum veya minimum olmayabilir.

  3. III. İfade: f' fonksiyonu x = 0 noktasında süreklidir.

    • Grafikte x = 0’da türev tanımlı ve süreklidir.

Doğru ifadeler:

  • Yalnız I ve III doğrudur.

Bu durumda doğru şık D) I ve III olacaktır.