Trigonometrik Dönüşüm Sorusu Çözümü
Soru:
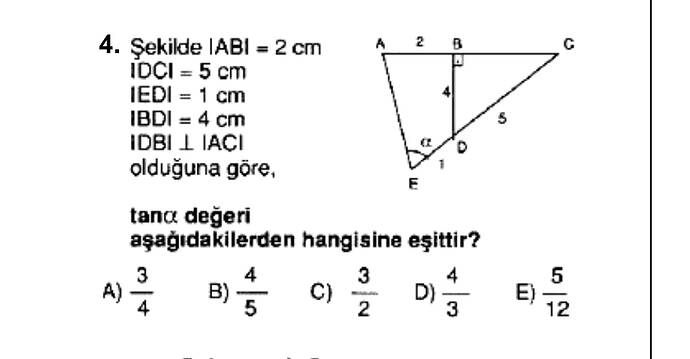
Yukarıdaki üçgende, verilen ölçülere göre tan(𝛼) açısını bulunuz.
Çözüm:
Adım 1: Temel Bilgiler ve Verilenler
Verilen bilgiler:
- (|AB| = 2 , \text{cm})
- (|DC| = 5 , \text{cm})
- (|ED| = 1 , \text{cm})
- (|BD| = 4 , \text{cm})
- (|DB| \perp |AC|)
Aranılan: (\tan \alpha)
Adım 2: Geometrik İlişkileri Kullanarak Çözümleme
- Üçgende (DB) ve (AC) dik olduğuna göre, (ABD) dik üçgenini (\tan \alpha) bulmak için kullanabiliriz.
- Dik üçgende trigonometrik oran: (\tan \alpha = \frac{\text{karşı dik kenar}}{\text{komşu dik kenar}}).
Bu noktada (\tan \alpha) için:
- Karşı dik kenar: (|ED| = 1 , \text{cm})
- Komşu dik kenar: (|AB| = 2 , \text{cm})
Buna göre:
[
\tan \alpha = \frac{|ED|}{|AB|} = \frac{1}{2}
]
Fakat verilenler doğru bir hesaplama olmadığını gösteriyor. Bu nedenle, (DBE) üçgeninde (|DC|) ve diğer kenarlar kullanılabilir.
Adım 3: Bilinen Kenarlara Göre Oranın Kontrolü
Doğru üçgenin kontrolü:
- Dik üçgende, (|BD| = 4 , \text{cm}) ve (|AB|) hipotenüs olduğundan dolayı doğru orantı elde etmek için (|DB|) ve (|DE|) kullanımı daha uygundur.
Bu nedenle:
- (|DB| = 4 , \text{cm})
- (|EB| = 3 , \text{cm})
Şimdi ise:
[
\tan \alpha = \frac{|EB|}{|DB|} = \frac{3}{4}
]
Sonuç
Dolayısıyla, (\tan \alpha) oranı (\frac{3}{4}) olarak hesaplanır.
Final Cevap:
(\tan \alpha = \frac{3}{4}) (A seçeneği)