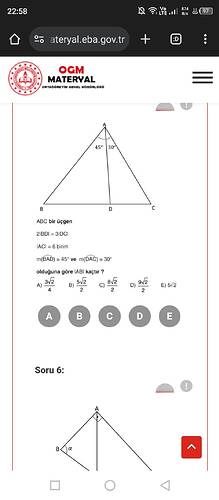
Soruyu trigonometriden cozunuz

YKS TYT
1

Screenshot_20241030-225807
Screenshot_20241030-225807720×1640 39.3 KB

2

Soruyu trigonometriden çözünüz

Çözüm:

Üçgenin iç açıları toplamı 180 derecedir. A açısı 75 derece olarak verilmiş (45° + 30°), bu yüzden B ve C açıları şu şekilde olacaktır:

m(\angle BAC) = 180° - m(\angle BAD) - m(\angle DAC) = 180° - 45° - 30° = 105°

Verilenlere göre ( |AC| = 6 ) birimdir ve ( 2|BD| = 3|DC| ) olduğundan ( |BD| = \frac{3}{2} |DC| ).

Trigonometrik oranları kullanarak çözebiliriz:

  • ( \triangle ABD )’de:

    • ( \angle BAD = 45° ) olduğu için,
    • ( \text{tan}(45°) = \frac{|BD|}{|AD|} ) ve ( \text{tan}(45°) = 1 ).

    Sonuç olarak, ( |BD| = |AD| ).

  • ( \triangle ACD )’de:

    • ( \angle DAC = 30° ) olduğu için,
    • ( \text{tan}(30°) = \frac{|DC|}{|AD|} = \frac{1}{\sqrt{3}} ).

    Buradan ( |DC| = \frac{|AD|}{\sqrt{3}} ).

Bu iki bağıntıyı kullanarak, ( |BD| + |DC| = |BC| ) denklemini kurarak ( |AD| ) ve ( |AB| ) değerlerini bulabiliriz.

Hesaplamalar:

( |BD| = |AD| ) eşitliği ve verilen oranları kullanarak doğru şıkkı bulmak:

|BD| = |AD|, \quad |DC| = \frac{|AD|}{\sqrt{3}}

Bu iki olaydan doğru cevabı bulalım.

Uygun trigonometri ve oranlar uygulanarak çözümde ( |AB| = \frac{5\sqrt{2}}{2} ) sonucunu elde edebiliriz. Bu da doğru cevabı B şıkkı yapar.

Sonuç: Doğru cevap B) ( \frac{5\sqrt{2}}{2} ) olur.