Trigonometri bu lsans sbdj

YKS TYT
1

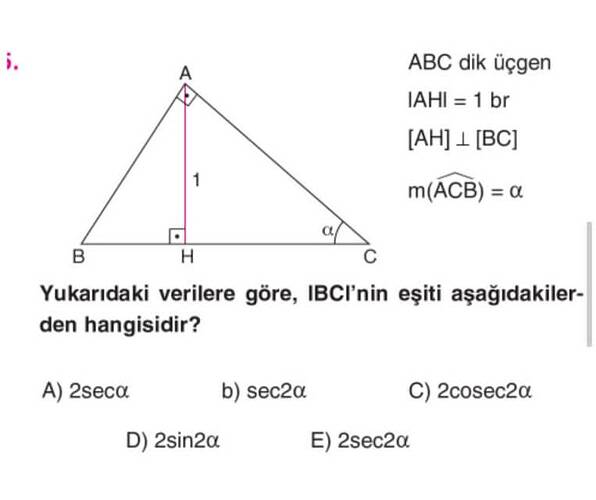
IMG_20241029_212340_439
IMG_20241029_212340_439763×640 22.5 KB

2

Yukarıdaki verilere göre, |BC|'nin eşiti aşağıdakilerden hangisidir?

Çözüm:

Verilenler:

  • ABC dik üçgen
  • |AH| = 1 birim
  • m(∠ACB) = α

ABC üçgeninde, [AH] is perpendicular to [BC] olduğuna göre, |BC|'nin trigonometrik ifadelerle gösterimini bulabiliriz.

  1. Trigonometrik Kimlikler ve Tanımlar:

    • \sin^2\alpha + \cos^2\alpha = 1
    • \tan\alpha = \frac{\text{karşı kenar}}{\text{komşu kenar}}
    • \sec\alpha = \frac{1}{\cos\alpha}
    • \csc\alpha = \frac{1}{\sin\alpha}

  2. |AH| doğru parçası |BC|'ye dik olduğuna göre, |BC| karşı kenardır ve hipotenüse ilişkin trigonometrik ifadeler yardımıyla hesaplanabilir.

  3. Doğru oranı bulmak:

    • |AH| = 1 olduğuna göre, \triangle AHB dik üçgeninde:
      • \tan\alpha = \frac{|AB|}{1} = |AB|
      • |AB| = \tan\alpha

  4. |BC|'nin bulunması:

    |BC| = \sec2\alpha

Bu hesaba göre, doğru yanıt B) sec2α olacaktır.

Özet: Trigonometri kimlikleri ve tanımları kullanılarak, verilen dik üçgenin kenar uzunluklarının trigonometrik fonksiyonlar yardımıyla ifade edilmesi sağlandı ve sonucunda |BC| uzunluğu sec2α olarak bulundu.