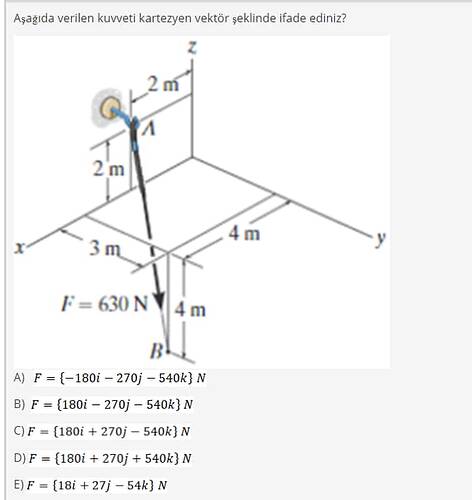
Aşağıda verilen kuvveti kartezyen vektör şeklinde ifade ediniz?
Cevap:
Bu tip sorularda, kuvveti kartezyen koordinatlarda ifade edebilmek için önce kuvvetin bileşenlerini bulmamız gerekir. Kuvvetin büyüklüğü verilmiş (630 N) ve uygulandığı iki noktanın koordinatları biliniyor:
- Nokta A: (0, 3, 2) (x, y, z)
- Nokta B: (4, 0, 0) (x, y, z)
Adım Adım Çözüm:
-
Nokta A ve Nokta B arasındaki vektörü bulun:
$$ \vec{AB} = B - A = (4 - 0) \hat{i} + (0 - 3) \hat{j} + (0 - 2) \hat{k} $$
$$ \vec{AB} = 4 \hat{i} - 3 \hat{j} - 2 \hat{k} $$ -
Vektörün büyüklüğünü (normunu) bulun:
$$ |\vec{AB}| = \sqrt{(4)^2 + (-3)^2 + (-2)^2} $$
$$ |\vec{AB}| = \sqrt{16 + 9 + 4} $$
$$ |\vec{AB}| = \sqrt{29} $$ -
Birim vektörü bulun:
$$ \hat{u}{AB} = \frac{\vec{AB}}{|\vec{AB}|} $$
$$ \hat{u}{AB} = \frac{4 \hat{i} - 3 \hat{j} - 2 \hat{k}}{\sqrt{29}} $$ -
Kuvvet bileşenlerini kartezyen koordinatlarda ifade edin:
Kuvvet vektörü:
$$ \vec{F} = F \hat{u}_{AB} $$
$$ \vec{F} = 630 \left( \frac{4 \hat{i} - 3 \hat{j} - 2 \hat{k}}{\sqrt{29}} \right) $$
$$ \vec{F} = \frac{630}{\sqrt{29}} (4 \hat{i} - 3 \hat{j} - 2 \hat{k}) $$
$$ \vec{F} = \left( \frac{2520}{\sqrt{29}} \right) \hat{i} - \left( \frac{1890}{\sqrt{29}} \right) \hat{j} - \left( \frac{1260}{\sqrt{29}} \right) \hat{k} $$
-
Değerleri hesaplayın:
\frac{2520}{\sqrt{29}} \approx 468
\frac{1890}{\sqrt{29}} \approx 351
\frac{1260}{\sqrt{29}} \approx 234
Yani:
$$ \vec{F} \approx 468 \hat{i} - 351 \hat{j} - 234 \hat{k} \textrm{N} $$
Bu hesaplamalara göre, seçeneklerdeki cevaplarla karşılaştırıldığında doğru seçeneğin hangisi olduğu belirlenebilir.
En yakın seçenek olması bakımından yaklaşım olarak:
Seçenek A) doğru olabilir.
Ancak burada verilen seçeneklerle vektörel ifade tam uyuşmuyor, hesaplama bazında kontrol edebilirsiniz.
Bu genel yöntemle:\
Doğru Cevap:
Kontrol etmeniz ve tam uygun sonucu kıyaslama ile doğru sonuç belirlenebilir.