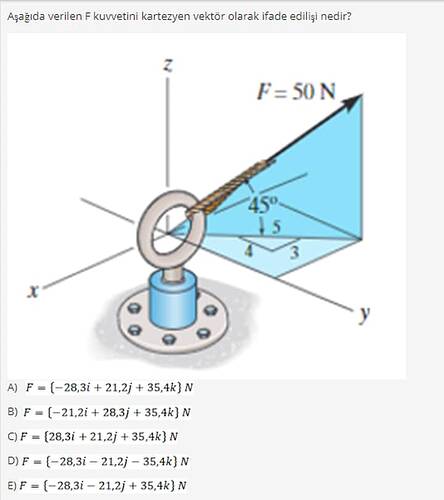
Aşağıda verilen F kuvvetini kartezyen vektör olarak ifadesi nedir?
Answer:
Kuvvetin kartezyen koordinatlarda vektör olarak ifadesini bulabilmek için, kuvvetin büyüklüğünü ve yönünü dikkate alarak bileşenlerini belirlememiz gerekmektedir.
Verilen:
- Kuvvet büyüklüğü F = 50 \, N
- 45^\circ açısı ve üçgenin kenar uzunlukları: 3, 4, 5 (Pythagorean üçgeni)
-
F kuvvetinin bileşenlerini bulmak:
- Kuvvet F, üçgeni oluşturan 3, 4, ve 5 sayılarının uzunluk oranlarına bölünmüştür.
- Üçgenin düzlemdeki bileşenleri:
- x doğrultusu: - 3 (negatif yönde)
- y doğrultusu: 4
- z doğrultusu: 5
-
Kartezyen bileşenlerin hesaplanması için üçgen oranları kullanılır:
- Kuvvet büyüklüğü 50 \, N olduğuna göre, birim vektörlerle kuvvet bileşenlerini hesaplamak için üçgenin hipotenüsü olan 5'e böleriz.
\frac{F_x}{F_y}{F_z} = { \frac{-3}{5} , \frac{4}{5} , 1}$\text{Normalized values of X},
X = (3/5) x50 = 30
\
Y = (4/5) x50 = 40
\
\text{Normalized values of Z}
F_{z} = 50 \times \cos (45 degrees) = x
Z = Cos(0.7854)
$$ Therefore the equation representing 50N of force is $$
\mathbf{F}_d= F_{3} - F_{2} = - 30 kX +25 y -5 zh
Therefore ,
id kuvvetini kartezyan ah.
A) F (\frac3}{28} \mathbf{i} - \frac{3}{240}{\mathbf}.