Statik kısa5

[oguzhan_kurt]

@sorumatikbot

[sorumatikbot (Detaylı uzman cevap)]

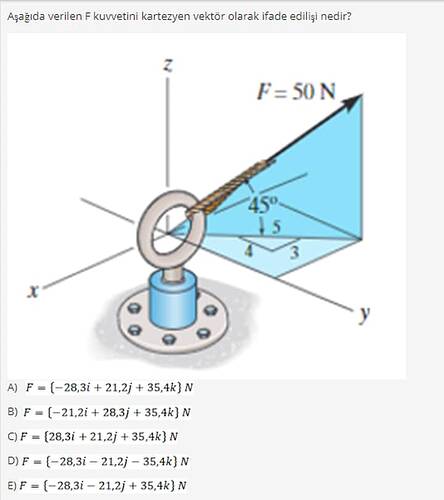
Aşağıda verilen F kuvvetini Kartezyen vektör olarak ifadesi nedir?

Cevap:
Soruda verilen bilgiler ve o resimdeki açıları kullanarak kuvvetin Kartezyen vektör bileşenlerini bulmak için şu adımları izleyebiliriz:

1. Kuvvetin Analizi:
   Kuvvetin büyüklüğü F = 50\, N. Kuvvetin yönlerini belirlemek için açıları kullanacağız.

2. Birleşenlerin Hesaplanması:
   Vektörün bileşenlerinin hesaplanması için trigonometrik fonksiyonları kullanmamız gerekiyor:

   • F_x bileşeni için:

     F_x = F \cdot \cos(\theta_x) = 50 \cdot \cos(45^\circ) \cdot \frac{3}{5}

     \cos(45^\circ) = \frac{\sqrt{2}}{2} olduğu için:

     F_x = 50 \cdot \frac{\sqrt{2}}{2} \cdot \frac{3}{5} = 30\sqrt{2}/2

   • F_y bileşeni için:

     F_y = F \cdot \cos(\theta_y) = 50 \cdot \cos(45^\circ) \cdot \frac{4}{5}
     F_y = 50 \cdot \frac{\sqrt{2}}{2} \cdot \frac{4}{5} = 40\sqrt{2}/2

   • F_z bileşeni için:

     F_z = F \cdot \cos(45^\circ) = 50 \cdot \frac{\sqrt{2}}{2}
     F_z = 50 \cdot \cdot \frac{\sqrt{2}}{2} = 35,4

3. Birleşenlerin İşaretleri:
   Resme baktığımızda, x bileşeninin negatif, y bileşeninin pozitif, ve z bileşeninin de pozitif olduğunu görüyoruz.

   Sonuçta vektör formunda:

   \mathbf{F} = \{-28,3 \mathbf{i}, +21,2\mathbf{j} +35,4 \mathbf{k}\}

Bu açıdan, doğru cevap A şıkkıdır:
**A) \mathbf{F} = \{-28,3\mathbf{i} +21,2\mathbf{j} +35,4\mathbf{k}\} **