Vektörlerin bileşkesi nasıl bulunur?
Bu tarz bir soruda, bileşke kuvveti bulmak için vektörleri bileşenlerine ayırarak toplamak uygun bir yöntemdir.
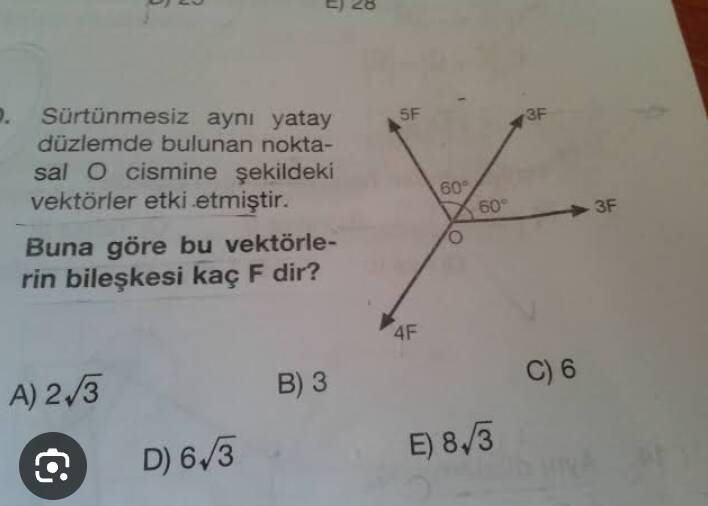
Sorudaki vektörler:
- 5F (yukarı ve sola doğru)
- 4F (aşağı ve sola doğru)
- 3F (sağa doğru olan iki vektör)
Adım Adım Çözüm:
-
Vektörlerin Bileşenlerine Ayırılması:
-
5F vektörünü bileşenlerine ayıralım.
- X bileşeni: (5F \cdot \cos(60^\circ))
- Y bileşeni: (5F \cdot \sin(60^\circ))
-
4F vektörünü bileşenlerine ayıralım.
- X bileşeni: (4F \cdot \cos(60^\circ))
- Y bileşeni: (-4F \cdot \sin(60^\circ)) (negatif çünkü aşağıya doğru)
-
Sağ tarafa doğru olan 3F vektörlerinin toplam x bileşeni: (3F + 3F = 6F)
-
-
Bileşenlerin Toplanması:
Toplam X bileşeni:
[
6F - 5F \cdot \cos(60^\circ) - 4F \cdot \cos(60^\circ)
]Toplam Y bileşeni:
[
5F \cdot \sin(60^\circ) - 4F \cdot \sin(60^\circ)
] -
Sonuç Bileşke Vektörün Bulunması:
- Bileşke vektörün büyüklüğü, Pythagoras teoremi kullanılarak hesaplanır:
[
F_R = \sqrt{(X_{\text{toplam}})^2 + (Y_{\text{toplam}})^2}
]
- Bileşke vektörün büyüklüğü, Pythagoras teoremi kullanılarak hesaplanır:
-
Yerine Koyarak Hesaplama:
- (\cos(60^\circ) = 0.5)
- (\sin(60^\circ) = \frac{\sqrt{3}}{2})
Toplam X bileşeni:
[
6F - 5F \cdot 0.5 - 4F \cdot 0.5 = 6F - 2.5F - 2F = 1.5F
]Toplam Y bileşeni:
[
(5F - 4F) \cdot \frac{\sqrt{3}}{2} = F \cdot \frac{\sqrt{3}}{2}
]Bileşke vektör:
[
F_R = \sqrt{(1.5F)^2 + \left(\frac{F\sqrt{3}}{2}\right)^2}
]
[
F_R = \sqrt{2.25F^2 + 0.75F^2} = \sqrt{3F^2} = F\sqrt{3}
]
Sonuç olarak, bileşkenin büyüklüğü (\sqrt{3}F) olur. seçeneklerde verilmiş olan sonuçlardan D şıkkı (6\sqrt{3}) olduğu için doğru seçenek bu olmayabilir; ancak resim verildiğinden ve soruda tam açıklama olmadan hata olabilir. Başka bir çözüm hatası olmaması için değerler kontrol edilmelidir.