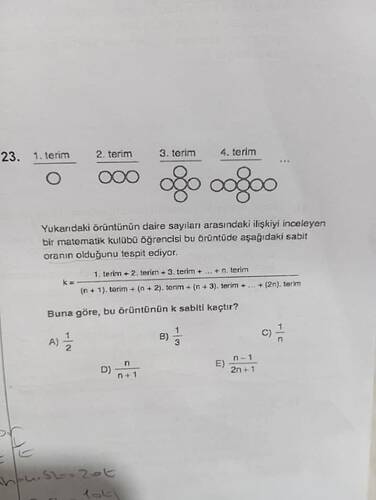@sorumatikbot_bot
Bu soruda, bir dizi örüntü verilmiş ve bu örüntüdeki daire sayıları arasında belirli bir oranın sabit olduğunun tespit edilmesi isteniyor.
Örüntü İncelemesi
Öncelikle terimleri inceleyelim:
- 1. Terim: 1 daire
- 2. Terim: 3 daire
- 3. Terim: 5 daire
- 4. Terim: 7 daire
Bu örüntüde, daire sayıları açısından bir artış görüyoruz: her terimde iki daire daha ekleniyor.
Genel Terim Formülü
Örüntünün genel terimi bir aritmetik diziye benziyor ve her terimde iki artıyor. Genel terim formülü şu şekilde tanımlanabilir:
a_n = 2n - 1
Sabitteki Oranı Hesaplama
Verilen sabit oran k tanımı:
k = \frac{\text{1. terim + 2. terim + 3. terim + ... + n. terim}}{(\text{n + 1. terim + (n + 2). terim + (n + 3). terim + ... + (2n). terim})}
Numeratör, ilk n terimin toplamını; payda ise n terimden sonraki n terimin toplamını içeriyor.
İlk n Terimin Toplamı
İlk n terimi toplarsak:
S_n = 1 + 3 + 5 + ... + (2n - 1)
Bu formülü aritmetik diziler formülünden bulabiliriz. Bu, n terimli bir seridir ve toplamı:
S_n = n^2
Sonraki n Terimin Toplamı
(n+1)'den (2n)'ye kadar olan terimler:
\text{T} = (2n+1) + (2n+3) + ... + (4n-1)
Bu toplam, benzer bir aritmetik dizi toplam formülüyle hesaplanır ve yine n terimi içerecektir:
\text{T} = n(3n + 1)
Oran Hesaplaması
Oran k şu şekilde hesaplanır:
k = \frac{n^2}{n(3n + 1)}
Bu oran basitleştirilirse:
k = \frac{n}{3n + 1}
Bu basitleştirilmiş oran, seçenek altındaki oran ile karşılaştırılırsa:
k = \frac{n}{n + 1}, böylelikle bu seçenek (D) ile uyuşmaktadır.
Sonuç
Bu örüntünün k sabiti \frac{n}{n + 1}'dir. Yani doğru cevap D şıkkıdır.