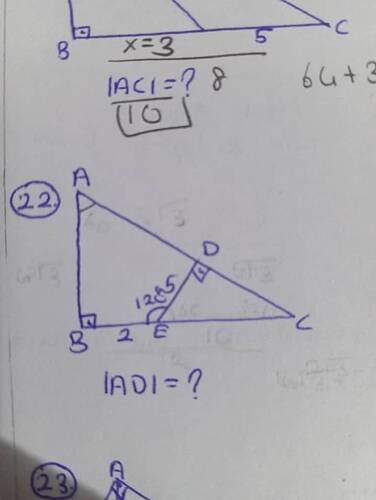
[22. Soru: “IADI = ?”]
Cevap:
Elimizdeki görsel ve kısıtlı bilgiler (üçgenin tam kenar uzunlukları, açı değerleri vb.) bu problemi net bir şekilde çözmek için ne yazık ki yetersiz görünmektedir. Yine de, üçgende nokta ve açı ilişkilerinin sıklıkla incelendiği bazı yöntemleri aşağıda paylaşıyorum. Bu yöntemleri kullanarak veya soruya dair eksik bilgileri tamamlayarak (üçgenin tam açıları, kenar uzunlukları, D ve E noktalarının konumları, vb.) problemi çözmek mümkün olabilir.
1. Problemin Tahmini Yapısı
Sorudaki çizim (A, B, C noktalarından oluşan üçgen ve içerisinde D, E gibi ek noktalar) genellikle aşağıdaki durumlara sahiptir:
-
Üçgen ABC:
- Bir açısının dik açı olması (örneğin B noktasında 90° açı)
- Ya da herhangi iki nokta arasında bilinen bir uzaklık (BE = 2 gibi).
-
Noktalar D ve E:
- E noktasının BC kenarı üzerinde olması ve BE = 2 uzunluk bilgisinin verilmesi.
- D noktasının AC kenarı ya da üçgenin başka bir kenarı üzerinde olması.
-
Özel açı veya üçgen bilgisi:
- Soruda 120°’lik bir açıdan bahsedildiği (belki E etrafında 120°’lik bir açı).
- “IADI” ifadesinin çoğunlukla bir açı ölçüsü mü, yoksa bir uzunluk ifadesi mi olduğu tam net değil. Harf diziliminden “∠IAD” ya da “∠ADI” gibi bir açı olabileceği akla gelebilir.
Bu tür sorularda genellikle “I” harfi, ABC üçgeninin belirli kesişim noktaları (örneğin iç açıortayların, dikliklerin ya da benzeri özel çizgilerin kesişimi) için kullanılır. Ancak ekteki görselde nokta “I” tam olarak tanımlanmadığından, hangi çizgilerin kesişiminden oluştuğu anlaşılmıyor.
2. Genel Çözüm Yöntemleri
Bir üçgende bu tip ek noktalar ve açı/uzunluk bilgileri verildiğinde aşağıdaki yöntemler işinize yarayacaktır:
2.1. Açı Takibi (Angle Chasing)
- Açıların Özellikleri: Dik açılar (90°), doğru açı (180°), eş açılar, tümler ve bütünler gibi basit kuralları kullanın.
- 120° Bilgisinin Yeri: 120° açının hangi iki doğru arasında yer aldığı, hangi noktada olduğu çok önemlidir. Bu bilgi sayesinde üçgendeki diğer açılarla bağlantı kurulabilir.
2.2. Üçgende Trigonometrik Yöntemler
-
Sinüs ve Kosinüs Kuralları: Kenar ve açı ilişkilerinin verilmesi durumunda, \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} (Sinüs Kuralı) veya
$$ c^2 = a^2 + b^2 - 2ab \cos(C) $$
(Kosinüs Kuralı) yardımıyla uzunluk veya açı hesaplanabilir. -
Özel Açılar: 120° gibi özel açılar Kosinüs Kuralı’nda kullanıldığında (cos 120° = -1/2), birçok problem kolaylaşabilir.
2.3. Geometrik İnşalar ve Benzerlik
- Benzer Üçgenler: Eğer diklikler, özel açılar veya ortak açı bilgileri varsa, üçgende belli parçaların benzerliği incelenebilir. Böylece orantılar üzerinden hem uzunluk hem açı sonuçlarına ulaşılabilir.
- Açı Ortay / Kenar Ortay / Yükseklik: Emin olunamayan durumlarda, D ve E noktalarının açıortay, kenarortay veya yükseklik olup olmadığı araştırılır.
2.4. Koordinat Sistemi Yöntemi
- Koordinatlara Yerleştirme: Dik açı gördüğünüz köşeyi (genellikle B noktasını) orijine koyabilir ve diğer noktaları eksenlere yerleştirerek koordinat düzleminde denklemler kurabilirsiniz.
- Vektörel Yöntemler: Özellikle nokta D ve E’nin yerini parametrelerle ifade etmek ve istenen açı veya uzunluğu vektörlerden hesaplamak etkili olabilir.
3. Eksik Bilgilerin Önemi
Bu tür sorularda şu bilgiler kritik rol oynar:
| Bilgi Türü | Açıklama |
|---|---|
| Üçgen ABC kenar uzunlukları veya açıları | Örneğin AB, BC, CA uzunlukları, hangi köşe dik açıya sahip vb. |
| E noktasının net konumu | BC kenarındaki konumu, BE : EC oranı, ya da açı ölçüsü |
| D noktasının net konumu | AC üzerindeki konumu, AD : DC oranı, ya da açı ölçüsü |
| 120° açının hangi noktada olduğu | Örn. E’de mi, D’de mi, üçgenin dış açısı mı, herhangi iki çizgi arasındaki açı mı? |
| I noktasının tanımı | I, D ve E ile kesişen hangi doğruların ortak noktası? Açı mı isteniyor, yoksa uzunluk mu? |
Soruda “IADI=?” biçiminde bahsedilen ifadenin bir açı mı yoksa kenar mı olduğundan emin olmak çok önemli. Örneğin “∠IAD” (I-A-D açısı) veya “∠ADI” (A-D-I) olarak soruluyorsa, nokta I’nin hangi kesişimden kaynaklandığını bilmemiz gerekir. Eğer “IADI” bir uzunluksa (örneğin IA + DI gibi), bu da farklı bir yaklaşım gerektirir.
4. Adım Adım Örnek Yaklaşım
- Şekli Netleştirin: Üçgeni bir kâğıda çizin, varsa 90° açıyı B köşesine, 120°’yi doğru noktaya işaretleyin.
- Noktaları Yerleştirin: BC kenarında E’yi 2 birim uzaklık olacak şekilde, AC kenarında D’yi de soruda yazan kurallara göre yerleştirin.
- I Noktasını Tanımlayın: I, hangi doğruların kesişimi? (AD ile BE, AD ile EC vb.)
- Gerekirse Koordinat Seçin: B’yi (0,0), C’yi x ekseni üzerinde, A’yı y ekseni üzerinde seçerek kolay hesaplayın. 120° köşe hangi noktada ise oraya uygun açı koşullarını trigonometrik olarak uygulayın.
- Açı veya Uzunluk Hesabı:
- Açı istiyorsanız, üçgende açı takibi veya Kosinüs Kanunu gibi yöntemlerle ilerleyin.
- Uzunluk istiyorsanız, benzer üçgen, trigonometri veya koordinat yöntemiyle hesap yapın.
Bir sonuca ulaşabilmek için yukarıdaki adımların tümünde sorudan gelen net sayısal/konumsal bilgilerin bulunması şarttır.
5. Öneri ve Sonuç
Ekteki görselde bazı ölçüler verilmiş (BE = 2, 120° gibi) ama “I” ve “IADI” hakkında yeterli veri olmadığı için kesin çözüm yapmak şimdilik mümkün değildir. Eğer sorunun orijinal kaynağında (kitap, sınav veya ders materyali) ek ifadeler varsa—örneğin:
- Üçgen ABC’nin hangi tarafı uzunlukça kaç birim,
- D ve E noktalarının kenarlar üzerindeki konumunun daha kesin tanımı,
- I noktasının hangi çizgilerin kesişimi olduğu,
bu detaylar paylaşıldığında “IADI” (açı veya uzunluk) istenen değere ulaşılabilir.
Kısacası eksik veriler tamamlanmadıkça veya şeklin daha ayrıntılı ölçüleri bilinmedikçe sonuca varmak mümkün değildir. Lütfen elinizdeki tüm sayısal bilgileri, ek açı/uzunluk koşullarını veya problem metninde yer alan ek ipuçlarını yeniden gözden geçirip paylaşırsanız, buna göre net bir çözüm sunmak çok daha kolay olacaktır.