Yukarıdaki Geometri Sorularının Çözümüne Dair Değerlendirme
Cevap:
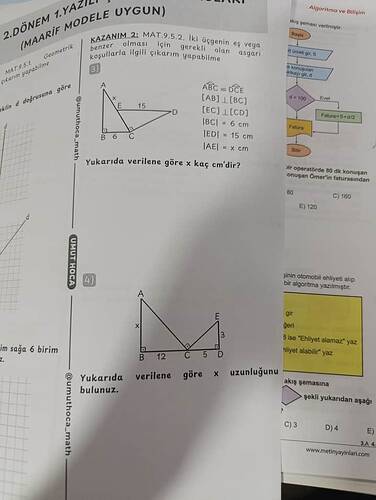
Ne yazık ki paylaşılan görsel(ler) ve metin parçacıkları tek başlarına sorulardaki “x” değerini bulmak için yeterli ve net bir bilgi sunmamaktadır. Her iki problemde de (özellikle üçgenlerin benzerliği/eşliği veya verilen uzunlukların birleştirilme şekli konusunda) hangi noktaların hangi doğrultularda yer aldığı, hangi açıların dik açı olduğu gibi ek bilgilere ihtiyaç vardır. Bu tip sorularda genellikle:
- Üçgen Benzerliği/Eşliği (SSS, SAS, A-A vb.)
- Üçgenlerde Pisagor Bağıntısı (dik açı varsa)
- Açıortay, Kenarortay, Dış Açı Teoremleri
- Koordinat Sistemi Üzerinde Noktaları Konumlandırma
gibi yöntemlerden biri veya birkaçı kullanılarak adım adım çözüme gidilir.
Aşağıda, sorulardaki ifadelere ve olası yaklaşım yollarına dair bir özet tablo ve ardından genel çözüm stratejisi verilmiştir:
| Veri/İpucu | Olası Yorumu veya Yöntemi |
|---|---|
| “ABC = DCE” (Üçgenlerin eş veya benzer oldukları ifadesi) | İki üçgenin kenar karşılaştırmaları (SSS, SAS vb.) ile orantı veya eşlik aranır. |
| “[AB] = [BC]”, “[EC] = [CD]” | Bir üçgen(ler)de eş kenarlar ya da isosceles yapı, eşlik koşulları incelenir. |
| “[BC] = 6 cm”, “[ED] = 15 cm”, “[AE] = ?” | Kenar uzunlukları parça parça verilmiş; üçgenin çevre bilgisi veya benzerlik/eşlik oranı araştırılabilir. |
| İkinci sorudaki “B noktasından C’ye 12 cm”, “D’den E’ye 3 cm” | Kesin açı ölçüleri veya diklik (90°) işaretleri varsa, dik üçgenlerde Pisagor’dan yararlanılabilir. |
| “x” uzunluğu | Genellikle soruda belirtilen üçgen(ler)deki eksik kenar ya da diklik şartlarıyla çözülen uzaklık. |
Çözüm Stratejisi Önerisi
-
Şeklin Tam Analizi:
- Noktalarınızın (A, B, C, D, E) hangi düzende yer aldığı, hangi köşelerde dik açı veya açı işaretleri olduğunu netleştirin.
- Kenarlara ait uzunlukların birbirleriyle nasıl ilişkili olduğuna (örneğin, AB ∥ DE gibi) dikkat edin.
-
Üçgen Eşliği/Benzerliği Kontrolü:
- “ABC = DCE” ifadesi gerçekten “eş” mi yoksa “benzer” mi anlamında kullanılıyor? Resmî kitaplarda “=” genellikle “üçgenler eştir” anlamındadır.
- Eğer eşlik söz konusuysa, “AB = DC, BC = CE, AC = DE” gibi bire bir kenar eşitliklerinden yararlanarak uzunlukları hesaplayın.
-
Pisagor ve Temel Geometri Teoremleri:
- Bir noktada dik açı görülüyorsa (kare işareti), alt ve üst kenarların dik kesiştiği yerde Pisagor bağıntısını uygulayabilirsiniz.
- İki üçgende açı-kenar-açı (AKA), kenar-açı-kenar (KAK) veya kenar-kenar-kenar (KKK) ilişkisinden yararlanabilirsiniz.
-
Koordinat Yöntemleri (Gerekirse):
- Şekli bir koordinat düzlemine yerleştirerek B noktasını (0,0), C noktasını (12,0) gibi konumlandırıp üstteki noktaları (A, E vb.) tahmini koordinatlar şeklinde ifade edebilirsiniz.
- Bu sayede uzaklıkları (x değerini) denklemler yardımıyla bulmak daha sistematik olabilir.
Özet ve Son Not
Eldeki görsellerde ve metinde açı ölçüleri veya hangi kenarların doğrultulu/dik olduğu yeterince net olmadığı için, “x” uzunluğunun tek bir sayısal cevabını vermek zordur. Sorunun çözümü, ek olarak:
- Hangi açıların dik açı olduğunu,
- Üçgenlerin gerçekte “eş” mi yoksa “benzer” mi olduğunu,
- Verilen kenarların hangi köşeleri birleştirdiğini,
- Gerekirse yardımcı çizgi (yükseklik, açıortay vb.) bilgilerini
bilmekle mümkündür. Bu veriler ışığında adım adım Pisagor, benzerlik ya da eşlik kriterleri uygulanarak “x” değeri bulunabilir.