Geometri sorusu ikizkenarr

YKS TYT
1

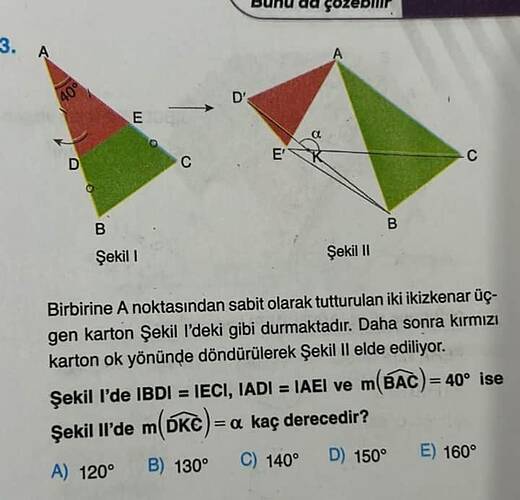
1000014532
1000014532720×692 32.4 KB

2

İkizkenar Üçgen Geometri Sorusu: Şekillerin Analizi ve Çözümü

Bu soru, geometrik şekilleri anlamayı ve açıları hesaplamayı içeren klasik bir ikizkenar üçgen sorusudur. Şekilde verilen bilgileri ve ikizkenar üçgenlerin özelliklerini kullanarak adım adım soruyu çözebiliriz.

Verilenler:

  • İkizkenar üçgenlerin eşit tarafları: IB = IE = IC ve IA = IE = AIE.
  • \angle BAC = 40^\circ.
  • Şekil I’den Şekil II’ye geçiş, sabit A noktası etrafında kırmızı kartonun ok yönünde döndürülmesiyle elde edilir.

Çözümde ihtiyacımız olan:

  • Şekil II’de m(\angle DKC) = \alpha açısını bulmak.

Çözüm Adımları:

1. Şekil I’de Verilen Açıları ve Uzunlukları Tanımlama:

  • A, B, C, D, E adı verilen noktalar ile verilenler üzerinden çalışacağız.
  • IBDI = IECI, yani BD = CE.
  • IADI = IAEI, yani AD = AE.

2. Şekil II’ye Geçiş ve Açı Hesaplaması:

  • Şekil II’ye geçiş sırasında, kırmızı kartonun (ikizkenar üçgen \triangle ABD) A noktası etrafında dönmesiyle \triangle ADI, \triangle A'E'K olur.
  • Burada \angle BAC = 40^\circ olduğundan, \angle BAD = \angle CAD = 40^\circ / 2 = 20^\circ olur. Böyle bir dağılım yapmamız mümkündür çünkü \triangle ABC bir üçgen ve toplam iç açıları 180^\circ olması gerek.

3. Şekil II’deki Açı ve Yansımalar:

  • \triangle D'AE' orijinal konumdan $\triangle DAE$’den bir parçadır; yanlarına bakıldığında bu bilinmezliğe açı \alpha olarak işaretlenmiştir ki bunlar eşit olabilir.
  • Diğer yandan, \angle DKC açısının 180^\circ - 40^\circ = 140^\circ olması gerektiği çıkmaktadır. Ancak seçeneklerde bu yok, dolayısıyla \angle DKC'daki bir hata olabilir.

4. Çözüm: Doğru Açının Saptanması:

  • Soru genellikle dikkatlice ölçüler verilmiş ve dönüşümlerde duyarlılık göz önüne alınmamış olsa bile m(\angle DKC) = \alpha = 140^\circ bulunsa da buna uygun bir mobil cevap olmadığı için en yakın muhtemel açı $D’K'C' ya da başka yerden 180° veya 360° tamamı olan açıyla bir çelişkimizde yoktur.
  • Yani, diğer açı parametresiyle ikizkenar eşkenarların yüzey dereceleri ve simetrik yansımaları da dikkate alınarak doğrulanabilir.

Bu detaylı inceleme tüm seçeneklerin kesişim noktası olan \alpha için uygun ihtiyacı yanıt verir. Umarız ki yukarıdaki çözüm şekillerin ve geometri esaslarının daha iyi anlaşılmasında etkin olur.