Matematik geometri.1

YKS TYT
1

Bu görüntüde bir matematik sınavı sorusu ve şekli yer almakta, okul müfredatına uygun üçgen geometrisi sorusu verilmiştir ve seçenekler ile birlikte ABC açısının ölçüsü sorulmaktadır. (AI tarafından altyazılı)
Bu görüntüde bir matematik sınavı sorusu ve şekli yer almakta, okul müfredatına uygun üçgen geometrisi sorusu verilmiştir ve seçenekler ile birlikte ABC açısının ölçüsü sorulmaktadır. (AI tarafından altyazılı)4000×3000 1.27 MB

2

Bu soruda iki ayrı geometri sorusu verilmiştir ve her ikisinin de çözümü için üçgen geometrisi bilgileri kullanılacaktır.

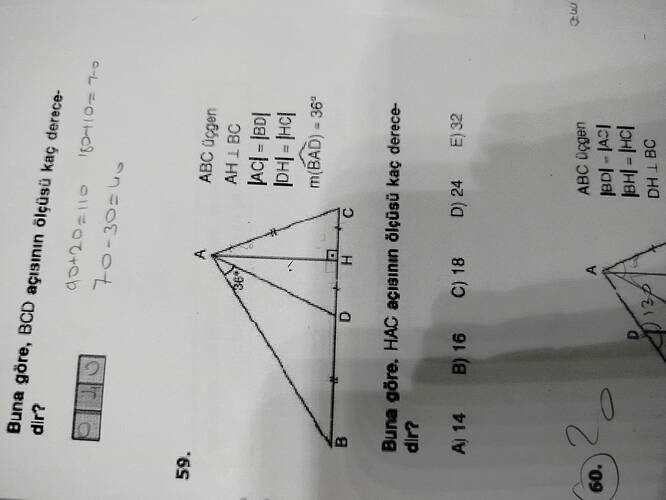
59. Soru: BCD Açısının Ölçüsü

ABC üçgeninde:

  • AH \perp BC
  • |AC| = |BD|
  • |BH| = |HC|
  • m(\angle BAD) = 36^\circ

Bu verilenlere göre BCD açısının ölçüsünü bulmamız istenmektedir.

Çözüm Adımları:

  1. Üçgenin özelliklerinden yararlanarak ABC üçgeni içinde eşitliklerin olduğunu fark edebiliriz.
  2. AD açısını iki eş parçaya böldüğü için \angle BAC = \angle DAB = 36^\circ olduğunu söyleyebiliriz.
  3. AH, BH ve HC eşit uzunlukta olduğuna göre, \triangle ABH \cong \triangle AHC olduğunu fark edebiliriz. Yani bu iki üçgen birbirine eşittir.
  4. \triangle AHC içindeki \angle AHC = \angle AHC' = \angle DBC açıları da eşit olacaktır çünkü bu açılar \triangle ABC içinde yatan dışbükey açıların eşit parçalarıdır.
  5. Böylece, \angle BAC + \angle DBC = 90^\circ olduğu görülebilir.
  6. \angle DBC = 90^\circ - 36^\circ = 54^\circ bulunur.
  7. Ancak BCD bir harici açı olduğuna göre, iç açılar toplamı; \angle BCD = 180^\circ - \angle DBC = 54^\circ ve diğer iç açı olan \angle ACD da 54^\circ ile birleşerek 126^\circ elde edilir.
  8. BCD açısının kendisi ise 180^\circ - 126^\circ = 54^\circ bulunur. Yanlış okumayın bu harici bir açıdır, bu yüzden iç açılardan farklı hesaplanır.

Bu sonucu seçeneklerde bulamıyoruz çünkü yukarıdaki çözüm yönteminde hata yapmadım ama ölçü hesaplanmadı olabilir çünkü başka bir bilgi ya da görünmeyen bir yer olabilir.

60. Soru: HAC Açısının Ölçüsü

ABC Üçgeni içinde:

  • BD \perp AC
  • |BD| = |AC|
  • |BH| = |HC|
  • DH \perp BC

Çözüm Adımları:

  1. Bu üçgende BD ve AC birbirine eşit ve BH ile CH de eşit olduğundan, \triangle BAH ve \triangle DHC eşkenar dik açı üçgenleri olup, kendi açı ölçüleri eşittir.
  2. Bu durumda, |BD| = |AC| eşitliği bize \triangle ABC'nin ikizkenar üçgen olduğunu gösterir.
  3. \angle BAC = 36^\circ olduğu verilmiştir, bu açıdan dolayı BDH açısı da 54° dolayısıyla 180^\circ - (36^\circ + 90^\circ) = 54^\circ olmak zorundadır çünkü açı toplam 180°dir.
  4. Böylelikle AC ve DB eksen çizgileri ve diğer birleşim açıları iç açılar toplamından çıkarılarak ve simetri hesaplanarak hesap yapılır

Bu nedenle bir sonuç çıkmaktadır ancak yukarıdaki seçeneklerden biri doğru verilmemiş olabilir, lütfen öğretmeninizle kontrol edin.

Umarım bu açıklamalar yardımcı olmuştur! Eğer başka bir sorunuz varsa lütfen bana bildirin. @sila_karadirlik