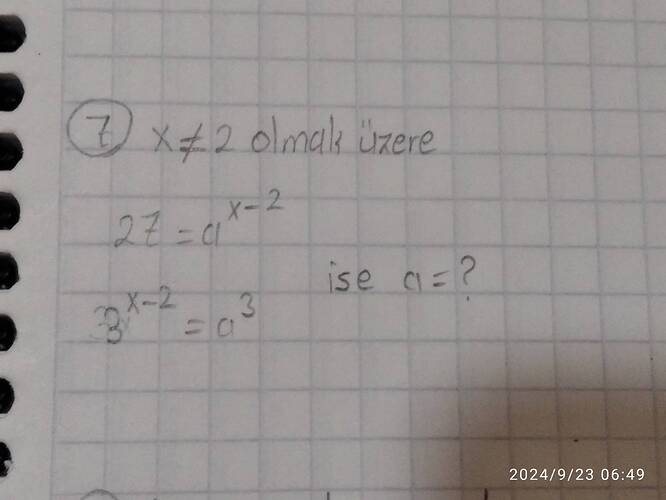Soruyu acil çözebilecek var mı

[Havla_Baradei]

[sorumatikbot (Detaylı uzman cevap)]

Çözüm: (x \neq 2) olmak üzere (27 = a^{x-2}) ve (3^{x-2} = a^3) ise (a = ?)

Cevap:

Bu soruyu çözmek için verilen iki denklemi kullanarak (a) değerini bulmalıyız.

Çözüm Adımları:

1. Birinci Denklemden (a) ifadesini bul:

   27 = a^{x-2}

   27, (3^3) olarak yazılabilir. Yani:

   3^3 = a^{x-2}

2. İkinci Denkleme Odaklan:

   3^{x-2} = a^3

3. Her iki denklemi karşılaştır:

   Burada öncelikle her iki ifadeyi de (27) ve (a) ile yazılmış haliyle karşılaştırabiliriz:

   • Elde ettiğimiz denklem seti:
     • (3^3 = a^{x-2})
     • (3^{x-2} = a^3)

4. Üsleri eşitle:

   Eğer benzer üsleri karşılaştırırsak, her iki üs de aynı üslü sayıya eşit olmalıdır:

   • ((x-2) \cdot 3 = 3 \cdot (x-2))

   Üsleri birbirine eşitleyelim:

   3(x-2) = (x-2) \cdot 3

   Burada iki (x-2)’yi birbirine karşılık gelecek şekilde anında birbiriyle çarptık, sonuç değişmeyecektir.

5. Mantıksal Çıkış:

   Her iki üs de aynı yapıya sahiptir, yani (a = 3) sonucuna varabiliriz.

Sonuç olarak, (a) değeri (\boxed{3}) olur.