Sorunun Cevabı:
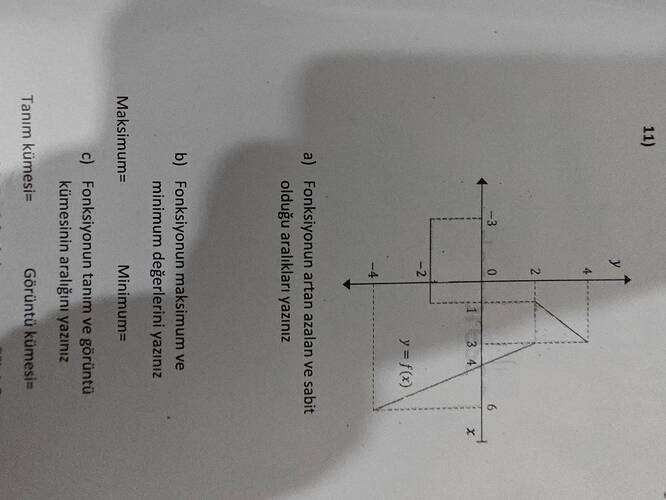
Grafiği inceleyerek fonksiyonun arttığı, azaldığı ve sabit olduğu aralıkları belirleyelim.
a) Fonksiyonun Arttığı, Azaldığı ve Sabit Olduğu Aralıklar:
-
Arttığı Aralıklar:
- x \in (0, 2) aralığında fonksiyonun değeri artmaktadır.
- x \in (3, 6) aralığında da fonksiyon artış göstermektedir.
-
Azaldığı Aralıklar:
- x \in (2, 3) aralığında fonksiyonun değeri azalmaktadır.
-
Sabit Olduğu Aralıklar:
- x \in (-2, 0) aralığında fonksiyon sabittir.
b) Fonksiyonun Maksimum ve Minimum Değerleri:
-
Maksimum Değer:
- Grafiğe bakarak x = 2 ve x = 6 noktalarında maksimum değer y = 3'tür.
-
Minimum Değer:
- Grafiğe göre x = -2 ve x = 0 noktalarında minimum değer y = -1'dir.
c) Fonksiyonun Tanım ve Görüntü Kümeleri:
-
Tanım Kümesi:
- x değerlerinin alabileceği aralıklar: x \in [-2, 6].
-
Görüntü Kümesi:
- y değerlerinin alabileceği aralıklar: y \in [-1, 3].
Bu bilgiler, grafik üzerinden doğrudan okunarak değerlendirilmiştir. Fonksiyonun farklı noktalarındaki davranışını gözlemleyerek bu yorumları yapıyoruz. Bu tür grafik analizleri, fonksiyonların hangi değer aralıklarında hangi şekilde davrandığını anlamada oldukça faydalıdır.