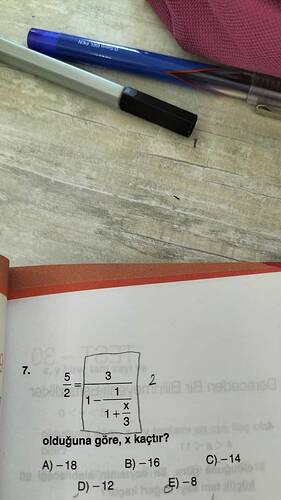
Soru: Verilen kesir ifadesi 5/2 değerine eşit olduğuna göre, x kaçtır?
Cevap:
Bu soruda görülen ifade, şu şekilde yorumlanabilir:
\frac{3}{\,1 - \frac{1}{\,1 + \tfrac{x}{3}\!}\!} = \frac{5}{2}.
Aşağıdaki adımları izleyerek x’i bulabiliriz:
-
Eşitliği basitçe kuralım:
\frac{3}{\,1 - \frac{1}{\,1 + \frac{x}{3}\!}\!} = \frac{5}{2}. -
Her iki tarafı çarpalım:
3 \times 2 = 5 \times \Bigl(1 - \frac{1}{\,1 + \frac{x}{3}\!}\Bigr).Bu işlem bize:
6 = 5 \times \Bigl(1 - \frac{1}{\,1 + \frac{x}{3}\!}\Bigr) -
Parantezi açıp sadeleştirelim:
\frac{6}{5} = 1 - \frac{1}{\,1 + \frac{x}{3}\!}. -
Her iki tarafta uygun düzenlemeler yaparak kesri yalnız bırakalım:
1 - \frac{6}{5} = \;-\frac{1}{5} \;=\; \frac{1}{\,1 + \frac{x}{3}\!}. -
Tersini alarak (payda-pay ilişkisi) çözelim:
1 + \frac{x}{3} = -5. -
Buradan x değerini bulun:
\frac{x}{3} = -6 \quad\Longrightarrow\quad x = -18.
x = -18 olduğunda kesir ifadesi tam olarak 5/2’yi verir. Dolayısıyla doğru yanıt -18’dir.
Aşağıdaki tabloda çözümün özet adımları gösterilmiştir:
| Adım | Yapılan İşlem | Sonuç |
|---|---|---|
| 1 | Eşitliği kurma | 3 / ( 1 - 1/(1 + x/3 ) ) = 5/2 |
| 2 | Her iki tarafa çarpma işlemi | 6 = 5 × ( 1 - 1/(1 + x/3 ) ) |
| 3 | \frac{6}{5} = 1 - \frac{1}{1 + x/3} açılması | 6/5 = 1 - 1/(1 + x/3) |
| 4 | Kesri yalnız bırakma | -1/5 = 1 / (1 + x/3) |
| 5 | Tersini alma | 1 + x/3 = -5 |
| 6 | x değerini bulma | x = -18 |