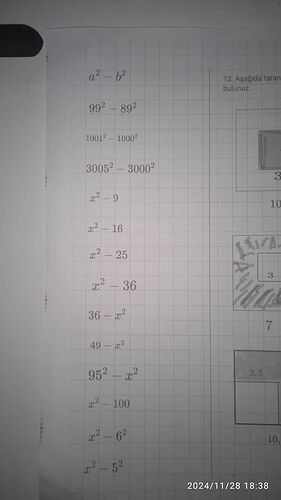
Görselde verilen matematik soruları, farkın karesi formülü kullanılarak çözülebilir. Formül, a^2 - b^2 = (a-b)(a+b) şeklindedir. Şimdi her bir ifadeyi bu formülü kullanarak çözelim:
-
99^2 - 89^2
$$(99 - 89)(99 + 89) = 10 \times 188 = 1880$$
-
1001^2 - 1000^2
$$(1001 - 1000)(1001 + 1000) = 1 \times 2001 = 2001$$
-
3005^2 - 3000^2
$$(3005 - 3000)(3005 + 3000) = 5 \times 6005 = 30025$$
-
x^2 - 9
$$(x - 3)(x + 3)$$
-
x^2 - 16
$$(x - 4)(x + 4)$$
-
x^2 - 25
$$(x - 5)(x + 5)$$
-
x^2 - 36
$$(x - 6)(x + 6)$$
-
36 - x^2
$$(6 - x)(6 + x)$$
-
49 - x^2
$$(7 - x)(7 + x)$$
-
95^2 - x^2
$$(95 - x)(95 + x)$$
-
x^2 - 100
$$(x - 10)(x + 10)$$
-
x^2 - 6^2
$$(x - 6)(x + 6)$$
-
x^2 - 5^2
$$(x - 5)(x + 5)$$
Bu şekilde çarpanlara ayırarak veya sayısal ifadeleri hesaplayarak soruları çözebiliriz. Her bir soru, farkın karesi formülüne uygun olarak çözüldü. Başka bir sorunuz olursa sormaktan çekinmeyin!