1. Özdeşlik Olan Denklemleri Belirleyin:
Özdeşlik, her durumda doğru olan bir eşitliktir. Aşağıdaki denklemlerin hangilerinin özdeşlik olduğunu belirleyelim.
- x + 2x = 3x: Bu bir özdeşliktir çünkü her gerçek sayı için doğrudur.
- x + x = x^2: Bu bir özdeşlik değildir; sadece belirli x değerleri için doğrudur (örneğin, x=0).
- a + b = ab: Bu bir özdeşlik değildir; her zaman doğru olmayan bir ifadedir.
- x.x.x.x = x^4: Bu bir özdeşliktir, çarpan sayısı 4 olduğu için.
- 3.(x + 1) = 3x + 1: Bu bir özdeşlik değildir; dağılım doğrusu farklıdır.
- x.(x - y) = x^2 - xy: Bu bir özdeşliktir; doğru bir şekilde dağıtılmıştır.
- 2.(3 + a) = 6 + 2a: Bu bir özdeşliktir; doğru bir şekilde dağıtılmıştır.
- (x + 2)^2 = x^2 + 2x - 4: Bu bir özdeşlik değildir; açılım yanlıştır.
- (a - 3)^2 = a^2 - 6a + 9: Bu bir özdeşliktir; doğru bir açılımdır.
2. İfadelerin Özdeşliklerini Bulun:
Her bir ifadeyi açıyoruz:
a) (x + 1)^2 = x^2 + 2x + 1
b) (x + 2)^2 = x^2 + 4x + 4
c) (2x + 1)^2 = 4x^2 + 4x + 1
d) (3x + 5)^2 = 9x^2 + 30x + 25
e) (4a + 3b)^2 = 16a^2 + 24ab + 9b^2
f) (y - 1)^2 = y^2 - 2y + 1
g) (a - 2)^2 = a^2 - 4a + 4
h) (7a - 8)^2 = 49a^2 - 112a + 64
i) (5 - x)^2 = 25 - 10x + x^2
j) (9x - 3y)^2 = 81x^2 - 54xy + 9y^2
İki kare farkını kullanarak özdeşlik oluşturma:
a) x^2 - 1 = (x - 1)(x + 1)
b) y^2 - 4 = (y - 2)(y + 2)
c) 4z^2 - 9 = (2z - 3)(2z + 3)
d) 36a^2 - 144b^2 = (6a - 12b)(6a + 12b) (Ortak çarpanları ayırarak basitleştirilebilir.)
e) 16n^2 - 9 = (4n - 3)(4n + 3)
f) 64 - x^2 = (8 - x)(8 + x)
g) (9a)^2 - 25 = (9a - 5)(9a + 5)
h) (2k)^2 - (3p)^2 = (2k - 3p)(2k + 3p)
g) 100 - 36x^2 = (10 - 6x)(10 + 6x)
h) 144a^2 - 49b^2 = (12a - 7b)(12a + 7b)
i) x^n - 1 ve x^n - x^1 gibi ifadeler faktörleme gerektirebilir, bu tür ifadeler genellikle özel teknikler veya başka kurallar kullanılarak çözülür.
Bu ifadelerde genel faktörleme kurallarını ve basitleştirmeleri kullanarak özdeşlikleri bulduk. Özdeşlikler, ifadelerin açılımı veya sadeleştirilmesi ile elde edilebilir. Her iki tür özdeşlik de matematikte yaygın ve fonksiyoneldir.
Aşağıdaki İfadelerin Özdeşliklerini Bulunuz:
a) (x - 3)(x + 3) = x^2 - 9
b) (2x + y)(2x - y) = 4x^2 - y^2
c) (3a - 5b)(3a + 5b) = 9a^2 - 25b^2
d) (7 - x)(7 + x) = 49 - x^2
e) (x + 6)(x + 6) = x^2 + 12x + 36
f) (2n + 4)(2n - 4) = 4n^2 - 16
g) (a - 2)(a - 2) = a^2 - 4a + 4
h) (x + 9)(x - 9) = x^2 - 81
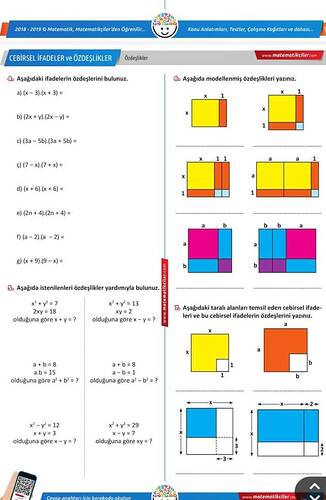
Modellemiş Özdeşlikler:
Görsellerdeki modeller genel olarak aşağıdaki şekilde temsil edilebilir:
- (x + 1)^2
- (a + 1)^2
- (a + b)^2
İstenen Özdeşlikler Yardımıyla Bulunuz:
-
x^2 + y^2 = 7, 2xy = 18 olduğuna göre x + y = ?
(x + y)^2 = x^2 + 2xy + y^2 = 7 + 18 = 25 \Rightarrow x + y = 5
-
x^2 + y^2 = 13, xy = 2 olduğuna göre x - y = ?
(x - y)^2 = x^2 - 2xy + y^2 = 13 - 4 = 9 \Rightarrow x - y = 3
-
a + b = 8, a \cdot b = 15 olduğuna göre a^2 + b^2 = ?
a^2 + b^2 = (a + b)^2 - 2ab = 64 - 30 = 34
-
a + b = 8, a - b = 1 olduğuna göre a^2 - b^2 = ?
a^2 - b^2 = (a + b)(a - b) = 8 \cdot 1 = 8
-
x^2 - y^2 = 12, x + y = 3 olduğuna göre x - y = ?
(x - y)(x + y) = 12 \Rightarrow (x - y) \cdot 3 = 12 \Rightarrow x - y = 4
-
x^2 + y^2 = 29, x - y = 7 olduğuna göre xy = ?
(x + y)^2 = x^2 + 2xy + y^2 = 29
x + y = \sqrt{29 - 2xy} ifadesini kullanarak denklemlerle çözülür.
Taralı Alanları Temsil Eden Cebirsel İfadeler:
- Sarı alan: x^2
- Turuncu alan: x \cdot 1 = x
- Mavi alan: 1 \cdot 1 = 1
Renklerle temsil edilen alanların toplamı cebirsel ifadelerin özdeşliklerini oluşturur. Bu tür modeller, cebirsel ifadelerin görselleştirilmesi ve anlaşılması açısından faydalıdır.