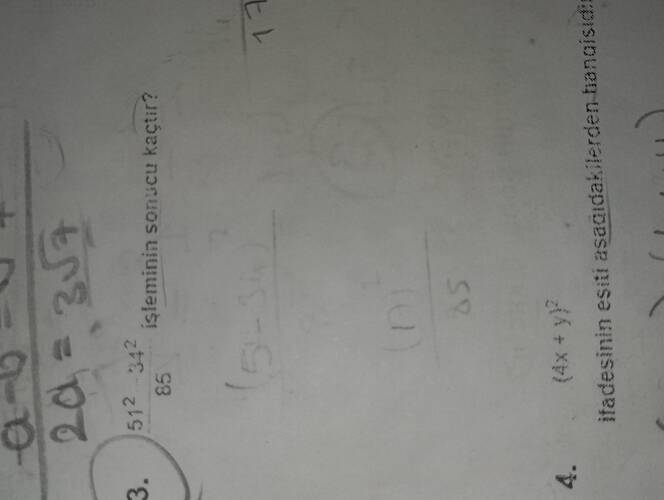Görseldeki matematik sorusunu okuyamıyorum, fakat matematik özdeşlikleriyle ilgili genel bir bilgi verebilirim.
Matematik Özdeşlikler
Özdeşlik Kavramı:
Özdeşlik, her değişken değeri için doğru olan eşitliklerdir. Örneğin:
-
Toplamların Karşılığı:
$$(a + b)^2 = a^2 + 2ab + b^2$$ -
Farkların Karşılığı:
$$(a - b)^2 = a^2 - 2ab + b^2$$ -
İki Kare Farkı:
$$a^2 - b^2 = (a - b)(a + b)$$
Bu özdeşlikler, polinomlar ve diğer matematiksel ifadelerin çözümlenmesinde sıkça kullanılır.
Ek Özdeşlikler ve Uygulamalar:
-
Küp Açılımlar:
- $$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$$
- $$(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3$$
-
Üslü İfadeler:
$$(a^2 - b^2) = (a - b)(a + b)$$
Daha karmaşık ifadeleri sadeleştirmek için kullanılır.
Özdeşliklerin Uygulama Alanları:
Matematikte özdeşlikler, karmaşık ifadeleri sadeleştirir ve denklem çözümleme gibi alanlarda kolaylık sağlar.
Aklınıza takılan başka bir matematik sorusu varsa sormaktan çekinmeyin!