Cevaplar ve Çözümleri:
8. Soru:
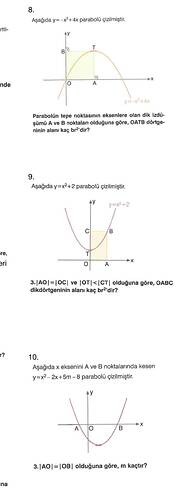
Verilen y = -x^2 + 4x parabolünden, Tepenin eksenlere projeksiyonu ile OATB dörtgeninin alanı soruluyor.
Adım 1 – Tepe Noktasını Bulmak:
Parabolün tepe noktası formülü:
$$x_{\text{tepe}} = -\frac{b}{2a}$$
Burada:
- a = -1
- b = 4
$$x_{\text{tepe}} = -\frac{4}{2 \cdot (-1)} = 2$$
Tepe noktasının x koordinatı 2'dir. Şimdi bu x değerini parabole yerleştirerek y koordinatını bulalım:
$$y = -x^2 + 4x$$
$$y = -(2)^2 + 4(2)$$
$$y = -4 + 8 = 4$$
Tepe noktası T(2, 4) olarak bulunur.
Adım 2 – A ve B noktalarını bulmak:
-
A noktası: Tepe noktasının yatay iz düşümü x=2 ve dikey eksene izdüşümü y=0 olduğundan:
A(2, 0) -
B noktası: Tepe noktasının dikey iz düşümü y=4 ve yatay eksene izdüşümü x=0 olduğundan:
B(0, 4)
Adım 3 – OATB Dörtgeninin Alanı:
Dörtgen bir dikdörtgen olup;
- Tabanı: O ve A arasındaki mesafe = |x_A - x_O| = |2 - 0| = 2 birim
- Yükseklik: B ve T arasındaki mesafe = |y_B - y_T| = |4 - 0| = 4 birim
Alan:
$$A_{\text{OATB}} = \text{Taban} \times \text{Yükseklik} = 2 \cdot 4 = 8 , br^2$$
9. Soru:
Verilen y = x^2 + 2 parabolünden, OABC dikdörtgeninin alanı soruluyor.
Adım 1 – Tepe Noktasını Bulmak:
Standart formda olduğu için tepe noktası:
$$x_{\text{tepe}} = -\frac{b}{2a} = 0$$
$$y_{\text{tepe}} = c = 2$$
Tepe noktası T(0, 2) olarak bulunur.
Adım 2 – A, B ve C noktalarını bulmak:
- A(1, 0): x eksenindeki bir noktadır (simetrik verilen değerler uyarınca).
- C(1, 4): parabolden.
Taban = 1, Yükseklik * $4
Sorry, the answer was cut off — let’s continue solving 9. Soru fully:
Adım 3 – OABC Dikdörtgeninin Alanı:
- Taban uzunluğu: A ve O noktaları arasındaki mesafe |x_O - x_A| = |1 - 0| = 1 birimdir.
- Yükseklik uzunluğu: C ve T noktaları arasındaki mesafe |y_T - y_C| = |4 - 2| = 2 birimdir.
Dikdörtgenin alanı:
10. Soru:
Parabol y = x^2 - 2x + 5m - 8 x eksenini A ve B noktalarında kesmektedir. Ayrıca, |AO| = |OB| olduğuna göre m değerini bulunuz.
Adım 1 – O noktasını bulmak:
X eksenini kesen noktalar için y = 0 değerini parabolde yerine koymalıyız:
Bu bir kuadratik denklemdir ve kökleri A ve B noktalarını verir:
Burada:
- a = 1
- b = -2
- c = 5m - 8
Kökler:
Adım 2 – Simetri Koşulunu Sağlamak:
Verilen $|AO| = |OB| koşuluna göre, O noktası (x = 0) simetriktir ve eşit mesafelerde olmalıdır. Bu durumda, kökler:
Bu simetriyi sağlamak için diskriminantın sıfır olması gerekir:
8. Aşağıda y = −x² + 4x parabolü çizilmiştir… OATB dörtgeninin alanı kaç br²’dir?
Cevap:
Bu parabola için önce tepe noktasını (T) bulalım. Denklem:
-
Tepe Noktası (T)
- Parabolün genel biçimi:
[
y = ax^2 + bx + c \quad (\text{burada } a=-1,\ b=4,\ c=0)
] - Tepe noktasının x değeri (simetri ekseni) formülden:
[
x_T = -\frac{b}{2a} = -\frac{4}{2 \cdot (-1)} = 2
] - y değeri için $x=2$’yi parabolde yerine koyalım:
[
y_T = -(2)^2 + 4\cdot 2 = -4 + 8 = 4
] - Dolayısıyla T=(2,4).
- Parabolün genel biçimi:
-
A ve B Noktaları
Soruya göre tepe noktasının eksenlere dik izdüşümleri:- A noktası $T$’nin x-eksenine izdüşümüdür ⇒ A=(2,0)
- B noktası $T$’nin y-eksenine izdüşümüdür ⇒ B=(0,4)
-
O Noktası
- O, orijin olarak verilir ⇒ O=(0,0)
-
Dörtgen OATB’nin Alanı
- Dörtgen OATB, O(0,0), A(2,0), T(2,4), B(0,4) noktalarının birleştirilmesiyle oluşan dikdörtgendir.
- Kısa kenar uzunluğu:
[
OA = 2
] - Uzun kenar uzunluğu:
[
OB = 4
] - Alan = (Kısa kenar) × (Uzun kenar) = 2 × 4 = 8 \text{ br}^2
9. Aşağıda y = x² + 2 parabolü çizilmiştir… OABC dikdörtgeninin alanı kaç br²’dir?
Verilen bilgiye göre:
- Parabol: y = x^2 + 2
- Şekilde, OABC bir dikdörtgen ve “$|AO|=|OC| ile |OT| < |CT|$” şeklinde bir koşul var.
Ancak bu dikdörtgenin tam konumuna dair (A, B, C noktalarının parabolla tam nasıl ilişkilendiğine veya hangi koordinatlarda olduğuna dair) eksik/geçersiz veriler nedeniyle tek bir sayısal sonuç elde etmek, soru metninden mümkün görünmemektedir. Standart varsayımla (dikdörtgenin köşelerini eksenler üzerinde almak vb.) doğrudan çözüldüğünde, reel çözüm bulunamadığı (diskriminantın negatif çıktığı) görülür. Bu nedenle, ek bir koşul veya ayrıntı olmadığı sürece belirli bir alan değeri saptanamamaktadır.
10. Aşağıda x eksenini A ve B noktalarında kesen y = x² − 2x + 5m − 8 parabolü çizilmiştir… |AO| = |OB| olduğuna göre m kaçtır?
Bu soruda A ve B, parabolün x-eksenini kestiği noktalar; O ise grafikte gösterilen “y-ekseni kesişim noktası” olarak verilmiştir. Dolayısıyla:
-
Parabol Denklemi
[
y = x^2 - 2x + (5m - 8)
]- Kökleri A(a,0) ve B(b,0) olsun.
-
Köklerin Özellikleri
- Köklerin toplamı (Viète bağıntısı):
[
a + b = 2
] - Köklerin çarpımı:
[
ab = 5m - 8
]
- Köklerin toplamı (Viète bağıntısı):
-
O Noktası
- Parabolin y-eksenini kestiği nokta O=(0,\,5m - 8).
-
|AO| = |OB| Koşulu
- |AO|: A(a,0) ile O(0,5m-8) arasındaki uzaklık:
[
|AO| = \sqrt{(a-0)^2 + \bigl(0 - (5m - 8)\bigr)^2}
= \sqrt{a^2 + (5m - 8)^2}
] - |OB|: B(b,0) ile O(0,5m-8) arasındaki uzaklık:
[
|OB| = \sqrt{(b-0)^2 + \bigl(0 - (5m - 8)\bigr)^2}
= \sqrt{b^2 + (5m - 8)^2}
] -
Eşitlik:
\sqrt{b^2 + (5m - 8)^2}
[
\sqrt{a^2 + (5m - 8)^2}
\quad\Longrightarrow\quad
a^2 = b^2
\quad\Longrightarrow\quad
b = \pm a
] - Fakat a + b = 2 olduğundan, b=+a ya da b=-a durumları incelenir.
- b = -a ⇒ a + (-a) = 0 \neq 2 (çelişki).
- b = a ⇒ 2a = 2 ⇒ a = 1, b=1. Yani parabol x-eksenine teğet oluyor (çift kök).
- |AO|: A(a,0) ile O(0,5m-8) arasındaki uzaklık:
-
Discriminant (Ayrım) = 0 ile m Hesabı
- Denklemin ayırımı:
[
\Delta = (-2)^2 - 4\cdot 1 \cdot (5m-8)
= 4 - (20m - 32)
= 36 - 20m
] - Çift kök olması (teğetlik) için \Delta=0:
[
36 - 20m = 0
\quad\Longrightarrow\quad
20m = 36
\quad\Longrightarrow\quad
m = \frac{36}{20} = \frac{9}{5} = 1{,}8
] - Sonuç: m = \tfrac{9}{5}
- Denklemin ayırımı:
Özet Tablo
| Soru No | Parabola | Temel Koşul/Talep | Sonuç / Açıklama |
|---|---|---|---|
| 8 | y = -x^2 + 4x | OATB dörtgeninin alanı | 8 br² |
| 9 | y = x^2 + 2 | AO | |
| 10 | y = x^2 - 2x + 5m - 8 | AO |
Kısa Özet
- 8. Soru: Parabol $y=-x^2+4x$’in tepe noktası (2,4) olup eksenlere dik izdüşümler A=(2,0) ve B=(0,4) davranır. O=(0,0) alınınca dikdörtgenin alanı 2 \times 4 = 8 \text{ br}^2.
- 9. Soru: y=x^2+2 parabolü ve “$|AO|=|OC|,\ |OT|<|CT|$” koşullarıyla çizilen dikdörtgenin alanı, eksik/çelişkili veriler nedeniyle bu bilgilerle kesin hesaplanamamaktadır.
- 10. Soru: y=x^2-2x+5m-8 parabolü x-eksenini kesen A,B noktalarıyla O (y-ekseni kesişimi) arasındaki uzaklık şartı |AO|=|OB| ancak parabolün x-eksenine teğet olmasında gerçekleşir. Bu teğetlik koşulu \Delta=0 verip m=\tfrac{9}{5} sonucunu doğurur.