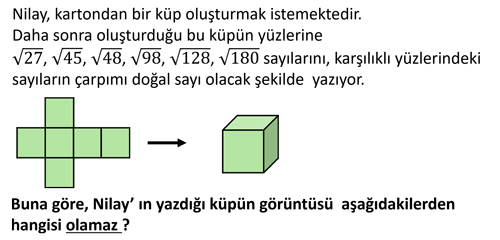
Soru:
Nilay, kartondan bir küp oluşturmak istemektedir. Daha sonra oluşturduğu bu küpün yüzlerine \sqrt{27}, \sqrt{45}, \sqrt{48}, \sqrt{98}, \sqrt{128}, \sqrt{180} sayılarını, karşılıklı yüzlerindeki sayıların çarpımı doğal sayı olacak şekilde yazıyor. Buna göre, Nilay’ın yazdığı küpün görüntüsü aşağıdakilerden hangisi olamaz?
Çözüm Süreci:
Adım 1: Sayıları İnceleyelim
Öncelikle verilen sayıların kökten çıkarılması ve sadeleştirilmesi gerekiyor:
- \sqrt{27} = \sqrt{3^3} = 3\sqrt{3}
- \sqrt{45} = \sqrt{3^2 \cdot 5} = 3\sqrt{5}
- \sqrt{48} = \sqrt{2^4 \cdot 3} = 4\sqrt{3}
- \sqrt{98} = \sqrt{2 \cdot 7^2} = 7\sqrt{2}
- \sqrt{128} = \sqrt{2^7} = 8\sqrt{2}
- \sqrt{180} = \sqrt{2^2 \cdot 3^2 \cdot 5} = 6\sqrt{5}
Adım 2: Doğal Sayı Olma Koşulu
Bu sayı çiftlerinden hangileri birbiriyle eşleştirilerek karşılıklı yüzlere yazıldığında çarpımları bir doğal sayı olur?
- 3\sqrt{3} ve 4\sqrt{3}: (Çarpım: 12) Doğal Sayı
- 3\sqrt{5} ve 6\sqrt{5}: (Çarpım: 18) Doğal Sayı
- 7\sqrt{2} ve 8\sqrt{2}: (Çarpım: 56) Doğal Sayı
Doğal sayı olan çarpımların elde edilebilmesi için bu eşleşmelerin yapılabileceğini görüyoruz.
Adım 3: Sonuç
Nilay, bu eşleştirmeleri yaparsa çarpımlar doğal sayı oluyor. Dolayısıyla bu çiftlerin karşılıklı geldiği durumlar geçerlidir. Herhangi farklı eşleştirmeler doğal sayı çarpımlar vermeyecektir. Yani, küpün yüzey yerleşimi bu çiftlerin dışında yapıldığında çarpımlar doğal sayı olmaz ve “görüntülerden hangisi olamaz” sorusunda çarpımları doğal sayı olmayan bir yerleşim olmalıdır.
Nihai Cevap:
Küp, verilen sayılar arasında yukarıda belirtiğimiz yerleşim dışında bir düzenle karşılaşıldığında görüntülerden biri olamaz. Çözümü olmayan yerleşim ise sayıları karşılıklı eşleştirmeden yerleştirmek olur. Bu durumda çarpım doğal sayı olmayacaktır ve bu durumda görüntü elde edilemez.