Soru başlığı mat

YKS TYT
1

1000012497
1000012497720×956 21.5 KB

2

Görseldeki soruları inceleyelim:

1. Soru

Hesaplama:

  1. Şekil 1 İçin Kullanılan Bant Uzunluğu:

    • 8 cm (yükseklik), 32 cm (genişlik), 64 cm (uzunluk)
    • Tüm yüzeyler için: 2 \times (8+32+64) = 208 cm

  2. Şekil 2 İçin Kullanılan Bant Uzunluğu:

    • 16 cm (yükseklik), 64 cm (genişlik), 128 cm (uzunluk)
    • Tüm yüzeyler için: 2 \times (16+64+128) = 416 cm

  3. Oran Bulma:

    • \frac{208}{416} = \frac{1}{2}

2. Soru

Tabloda sarı kutudan başlayarak kutunun içindeki sayı pozitifse sağa, negatifse aşağı hareket ediliyor ve gidilen kutudaki sayı ile çarpılıyor.

Tabloda ilerleme:

  1. Sarı kutudaki sayı: (-2)^1 = -2 (Aşağı)
    1. satır, 1. sütundaki sayı: (-2)^1 = -2 (Aşağı)
    1. satır, 1. sütundaki sayı: (-2)^{-2} = \frac{1}{4} (Sağa)
    1. satır, 2. sütundaki sayı: (-2)^{-2} = \frac{1}{4} (Sağa)
    1. satır, 3. sütundaki sayı: (2)^2 = 4 (Sağa)
    1. satır, 4. sütun (Numara IV)

Sonuç:

  • Şıkları değerlendirdiğimizde, doğru cevap IV olacaktır.

Bu hesaplamalarla ilgili soruların çözümlerini daha iyi anlamış olduk!

3

1000012498
10000124984080×3072 288 KB

4

Görseldeki soruları inceleyelim:

3. Soru

Verilen ifadeyi basitleştirelim: 2^{-3} ve (\frac{1}{8})^{-1}

Hesaplama:

  1. 2^{-3} = \frac{1}{2^3} = \frac{1}{8}
  2. (\frac{1}{8})^{-1} = 8

Sonuç 8 olduğuna göre, 8 ifadesi 2^3'e eşittir. Doğru cevap B) 2^3

4. Soru

6^{3}:(3^3 \cdot 4^{3})

Hesaplama:

  1. 6^3 = (2 \cdot 3)^3 = 2^3 \cdot 3^3
  2. Bölme ifadesinde: \frac{2^3 \cdot 3^3}{3^3 \cdot 4^3} = \frac{2^3}{4^3}
  3. \frac{2^3}{4^3} = \frac{8}{64} = \frac{1}{8} = 2^{-3}

Sonuç, doğru cevap C) 2^{-3}

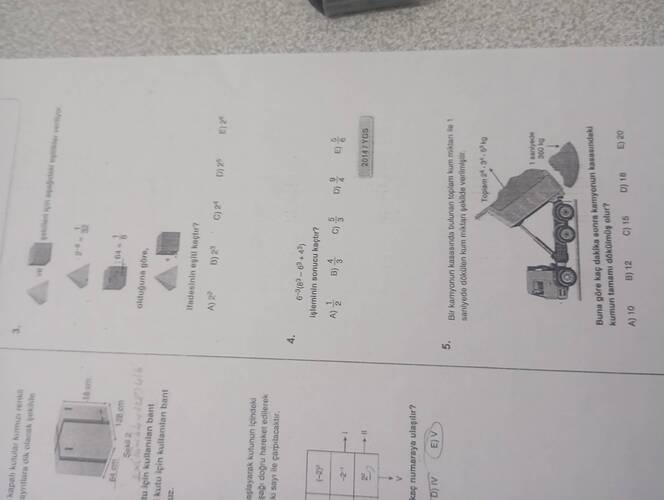
5. Soru

Her saniyede dökülen kum miktarı 500 kg ve kamyonun kasasında bulunan toplam kum 3^6 \cdot 3^3 kg olarak verilmiş.

Hesaplama:

  1. Toplam miktar: 3^6 \cdot 3^3 = 3^{9}
  2. 3^9 = 19683 kg
  3. Her saniyede 500 kg dökülüyor ve dakika bazında, 1 dakika 60 saniye olduğu için 60 \times 500 = 30000 kg dökülür.
  4. Kamyonun içindeki toplam kum miktarı 19683 kg olduğuna göre, tamamı dolmadan dökülebilir.

Sonuç: Yaklaşık 40 saniye sonra kamyonun içindeki kum biter.

Bu sorular ile ilgili hesaplamaları tamamladık!

5

1000012499
10000124994080×3072 371 KB

6

Görseldeki soruları inceleyelim:

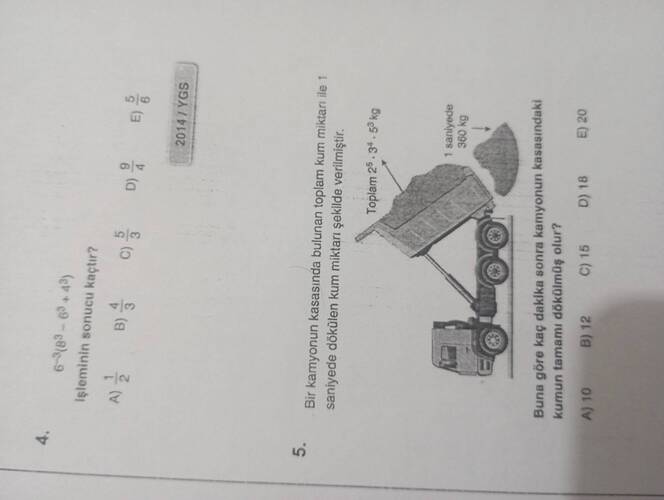
4. Soru

$$6^{-3} \div (8^{-3} - 6^{-3} + 4^{-3})$$ işlemini hesaplayalım.

Hesaplama:

  1. 6^{-3} = \frac{1}{6^3}
  2. 8^{-3} = \frac{1}{8^3}
  3. 4^{-3} = \frac{1}{4^3}

Parantez içi hesaplama:

  • \frac{1}{8^3} - \frac{1}{6^3} + \frac{1}{4^3}

Ortak payda bulma:

  • Ortak payda 8^3 \cdot 6^3 \cdot 4^3 olarak alınabilir.

Sonrasında hesaplama yaparak sonucu bulmanız gerekmektedir.

5. Soru

Kamyonda bulunan bütün kum miktarı: 2^5 \cdot 3^4 \cdot 5^3 kg

1 saniyede dökülen kum miktarı: 360 kg

Hesaplama:

  1. Toplam kum miktarı: 2^5 \cdot 3^4 \cdot 5^3
  2. Her saniye 360 kg dökülüyor.

360 kg’nın asal çarpanlar çarpanları: 2^3 \cdot 3^2 \cdot 5

Oranın hesabı:

  • Kamyon tamamen doldukça, kaç saniye geçeceğini hesaplamak gerekiyor.
  • Toplam kum miktarından ve dökülme hızından bu oran bulunabilir.

Her iki hesaplama için, daha detaylı matematiksel işlemler yaparak sonuç bulunabilir.