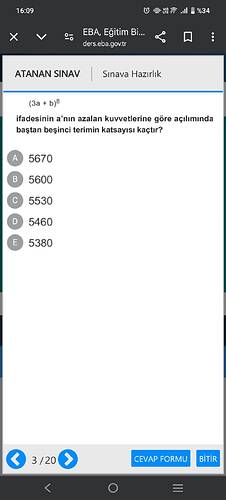
(3a + b)^8 ifadesinin a’nın azalan kuvvetlerine göre açılımında baştan beşinci terimin katsayısı kaçtır?
Temel Kavram
Bu tür sorular, binom açılımını ve binom katsayılarını içerir. Binom açılımı, (x + y)^n ifadesinin açılımı olup, genel terim (^nC_r) \cdot x^{(n-r)} \cdot y^r formülü ile bulunur. Burada ^nC_r, “n’in r’lisi” olarak adlandırılan kombinasyon ifadesidir.
Temel Cevap
Binom açılımı, her terimin katsayısını bulmak için kullanılan kombinasyonlarla çalışmayı gerektirir.
1. Adım: Binom Formülü ve Terim Belirleme
- Binom açılımının genel terimi: T_{r+1} = (^nC_r)(x^{n-r})(y^r)
2. Adım: Beşinci Terimin Hesaplanması
- Çözüm için n = 8 ve x = 3a, y = b.
- Başlangıçtan beşinci terim, T_5 ifadesi olacaktır. Bu da r = 4 anlamına gelir.
- Genel terim: T_{r+1} = (^8C_4)(3a)^{8-4}(b^4)
3. Adım: Katsayıları Hesapla
- T_5 = (^8C_4) \cdot (3a)^4 \cdot b^4
- ^8C_4 ifadesi, “8’in 4’lüsü” kombinasyonunu ifade eder.
4. Adım: Kombinasyon Hesabı
- ^8C_4 = \frac{8!}{4!(8-4)!} = \frac{8 \cdot 7 \cdot 6 \cdot 5}{4 \cdot 3 \cdot 2 \cdot 1} = 70
5. Adım: Tüm Terimler İçin Katsayı Hesapla
- T_5 = 70 \cdot (3)^4 \cdot a^4 \cdot b^4
- (3)^4 = 81
Son Cevap
- T_5 katsayı: 70 \cdot 81 = 5670
Beşinci terimin katsayısı: 5670 @Goksu_Kezer.