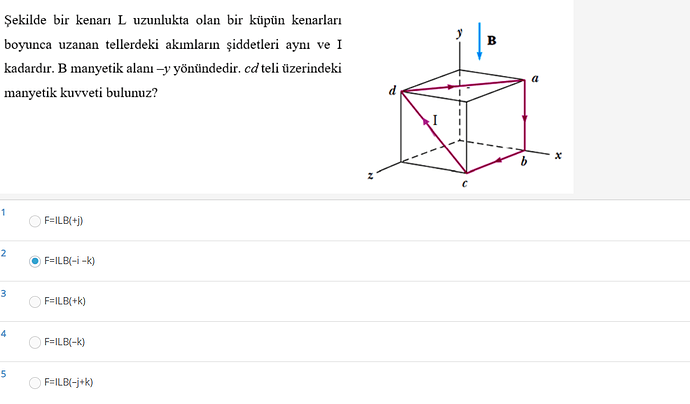
Şekilde bir kenarı L uzunlukta olan bir küpün kenarları boyunca uzanan tellerdeki akımların şiddetleri aynı ve I kadardır. B manyetik alanı -y yönündedir. cd teli üzerindeki manyetik kuvveti bulunuz?

Üniversite Üniversite Fizik
1

SDASDSADSADAS
SDASDSADSADAS1232×722 72.4 KB

2

Şekilde bir kenarı L uzunlukta olan bir küpün kenarları boyunca uzanan tellerdeki akımların şiddetleri aynı ve I kadardır. B manyetik alanı -y yönündedir. cd teli üzerindeki manyetik kuvveti bulunuz?

Cevap:
Bu soru, manyetik alan ve akım taşıyan teller arasındaki kuvvet ilişkisini anlatmakta. Bir tel üzerinde akım geçtiğinde, manyetik alan bir kuvvet uygulayacaktır. Bu kuvvetin yönü ve büyüklüğü, Lorentz Kuvveti’ne göre belirlenir:

\mathbf{F} = I (\mathbf{L} \times \mathbf{B})

Burada \mathbf{F}, kuvvet; I, akım; \mathbf{L}, teli temsil eden uzunluk vektörü; ve \mathbf{B}, manyetik alandır. Verilen durumda:

  • I: Akım
  • \mathbf{B}: Manyetik alan, -y yönünde
  • \mathbf{L}: Telin yönü ve uzunluğu, cd boyunca

1. Adım: \mathbf{L} Vektörünü Bulmak

cd teli, köşeleri c ve d olan kübün köşegeninde uzanmaktadır. Bu durumda uzunluk vektörü \mathbf{L}, c den d’ye olan pozisyon vektörü farkıyla verilebilir:

  • c köşesinin koordinatları: (0, 0, 0)
  • d köşesinin koordinatları: (L, L, L)

Bu durumda \mathbf{L} vektörü:

\mathbf{L} = L (\mathbf{i} + \mathbf{j} + \mathbf{k})

2. Adım: \mathbf{B} Vektörünü Kullanarak Çapraz Ürünü Bulmak

Manyetik alan -y yönündedir, yani \mathbf{B} = -B\mathbf{j}.

Çapraz çarpım \mathbf{L} \times \mathbf{B} şu şekilde hesaplanır:

\mathbf{L} \times \mathbf{B} = L (\mathbf{i} + \mathbf{j} + \mathbf{k}) \times (-B \mathbf{j})

Bileşenlere göre hesaplayalım:

L (\mathbf{i} \times -B \mathbf{j} + \mathbf{j} \times -B \mathbf{j} + \mathbf{k} \times -B \mathbf{j})

Çapraz çarpımlar:

\mathbf{i} \times \mathbf{j} = \mathbf{k}, \quad \mathbf{j} \times \mathbf{j} = 0, \quad \mathbf{k} \times \mathbf{j} = -\mathbf{i}

Bu yüzden:

\mathbf{L} \times \mathbf{B} = L (-B \mathbf{k} - B\mathbf{i})
\mathbf{L} \times \mathbf{B} = -LB (\mathbf{i} + \mathbf{k})

3. Adım: Kuvveti Bulmak

Kuvvet formülüne göre:

\mathbf{F} = I (\mathbf{L} \times \mathbf{B})

Yukarıdaki sonuca göre:

\mathbf{F} = I (-LB (\mathbf{i} + \mathbf{k}))
\mathbf{F} = -ILB (\mathbf{i} + \mathbf{k})

Sonuç:

cd teli üzerindeki manyetik kuvvet:

\mathbf{F} = I L B (-\mathbf{i} - \mathbf{k})

Bu durumda doğru seçenek F = ILB(-i - k) yani 2. seçenek olacaktır.