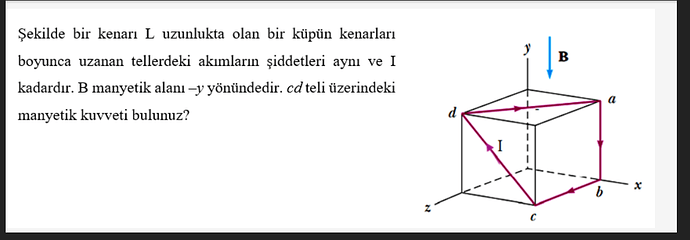
Şekilde bir kenarı L uzunlukta olan bir küpün kenarları boyunca uzanan tellerdeki akımların şiddetleri aynı ve I kadardır. B manyetik alanı –y yönündedir. CD teli üzerindeki manyetik kuvveti bulunuz?
Cevap:
Bu problemde, manyetik alan içinde bulunan ve akım taşıyan bir telin üzerindeki manyetik kuvveti analiz edeceğiz. Bu kuvvet, Biot-Savart Kanunu ve Lorentz Kuvvet Kanunu kullanılarak hesaplanabilir.
Adım 1: Telin Koordinatları ve Akım Yönleri
- Telin L uzunlukta olduğunu ve akımın yönünü cd teli boyunca olduğunu kabul edelim.
- Manyetik alan ( \mathbf{B} ) ise, negatif y yönünde olup ( \mathbf{B} = (0, -B, 0) ) şeklindedir.
Adım 2: Lorentz Kuvvet Kanunu
- Bir tel üzerindeki manyetik kuvvet ( \mathbf{F} = I (\mathbf{L} \times \mathbf{B}) ) olarak hesaplanır.
- L burada telin uzunluğunu ve yönünü (yani (\mathbf{L})) tanımlar.
Adım 3: Telin Uzunluğunun Vektör Şeklinde İfadesi
- ( \mathbf{L} ) vektörü c’den d’ye uzanan telin uzunluğunu ve yönünü göstermelidir.
- Koordinatlar c(0, 0, 0) ve d(L, L, 0) olduğu için, ( \mathbf{L} ) vektörü ( (L, L, 0) ) olur.
Adım 4: Manyetik Kuvvetin Hesaplanması
- Lorentz kuvvet formulüne göre ( \mathbf{F} = I (\mathbf{L} \times \mathbf{B}) )
- Burada ( \mathbf{L} = (L, L, 0) ) ve ( \mathbf{B} = (0, -B, 0) )
\mathbf{L} \times \mathbf{B} = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
L & L & 0 \\
0 & -B & 0 \\
\end{vmatrix}
- Determinantı hesaplarken:
\mathbf{L} \times \mathbf{B} = \mathbf{i}(L \cdot 0 - 0 \cdot -B) - \mathbf{j}(L \cdot 0 - 0 \cdot 0) + \mathbf{k}(L \cdot -B - L \cdot 0)
\mathbf{L} \times \mathbf{B} = \mathbf{k}(-LB) = -LB \mathbf{k}
- Bu durumda,
\mathbf{F} = I (\mathbf{L} \times \mathbf{B}) = I(-LB \mathbf{k}) = -ILB \mathbf{k}
Sonuç:
CD teli üzerindeki manyetik kuvvet -z yönünde ve büyüklüğü ( \mathbf{F} = -ILB \mathbf{k} ).
Yani, kuvvetin vektörel gösterimi ( \mathbf{F} = -ILB \mathbf{k} ) olacaktır.