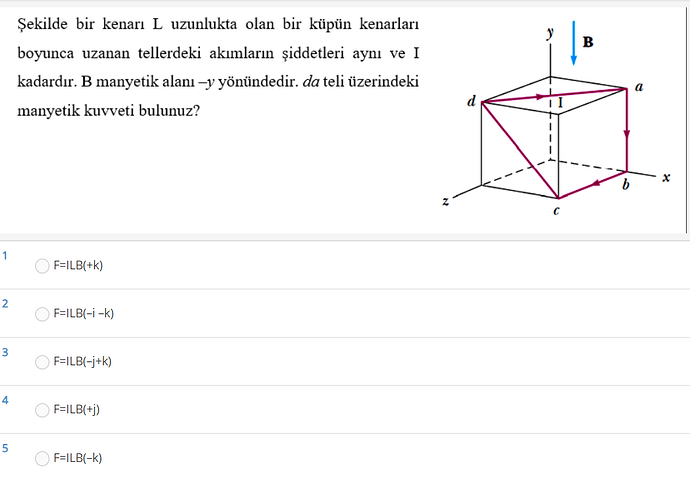
Şekilde bir kenarı L uzunlukta olan bir küpün kenarları boyunca uzanan tellerdeki akımların şiddetleri aynı ve I kadardır. B manyetik alanı –y yönündedir. da teli üzerindeki manyetik kuvveti bulunuz.
Cevap:
Manyetik alanda bir tel parçası üzerinde etki eden manyetik kuvvet, Lorentz kuvvet yasasına göre hesaplanır. Bu yasaya göre kuvvetin büyüklüğü ve yönü şu ifade ile verilir:
\mathbf{F} = I (\mathbf{L} \times \mathbf{B})
Burada:
- \mathbf{F} manyetik kuvvet,
- I telden geçen akım,
- \mathbf{L} telin uzunluğu ve yönü vektörü,
- \mathbf{B} manyetik alan vektörüdür.
Adım 1: Manyetik Alan Vektörü
Manyetik alan \mathbf{B}, -y yönünde olup \mathbf{B} = -Bj şeklinde ifade edilir.
Adım 2: Telin Uzunluk Vektörü
\mathbf{da} teli, d noktasından a noktasına gider. d noktası ((0, L, L)) ve a noktası ((L, L, 0)) şeklindedir.
Bu noktalar arasındaki uzunluk vektörü \mathbf{L} şu şekilde hesaplanır:
\mathbf{L} = (L - 0)\mathbf{i} + (L - L)\mathbf{j} + (0 - L)\mathbf{k}
Yani:
\mathbf{L} = L\mathbf{i} - L\mathbf{k}
Adım 3: Kuvvetin Hesaplanması
Kuvvet, \mathbf{L} ve \mathbf{B} vektörlerinin çapraz çarpımıyla bulunur:
\mathbf{F} = I (\mathbf{L} \times \mathbf{B})
Bununla ilgili çapraz çarpımı hesaplayalım:
\mathbf{L} \times \mathbf{B} = (L\mathbf{i} - L\mathbf{k}) \times (-B\mathbf{j})
- Bu çapraz çarpımı hesaplarken, vektörel çarpımın dağıtma özelliğini kullanabiliriz:
\mathbf{i} \times \mathbf{j} = \mathbf{k}, \quad \mathbf{k} \times \mathbf{j} = -\mathbf{i}
(L\mathbf{i} \times -B\mathbf{j}) + (-L\mathbf{k} \times -B\mathbf{j})
- LB\mathbf{k} + LB\mathbf{i}
Sonuç olarak:
\mathbf{F} = I (\mathbf{L} \times \mathbf{B}) = I( LB\mathbf{i} - LB\mathbf{k} )
$$= ILB(\mathbf{i} - \mathbf{k})
Aşağıdaki şıklar arasından, bu sonucu doğrulayan seçeneği seçeriz.
- Şık 2: F = ILB(–i –k)
Sonuç olarak, doğru cevap **2: F=ILB(–i –k)** olacaktır.