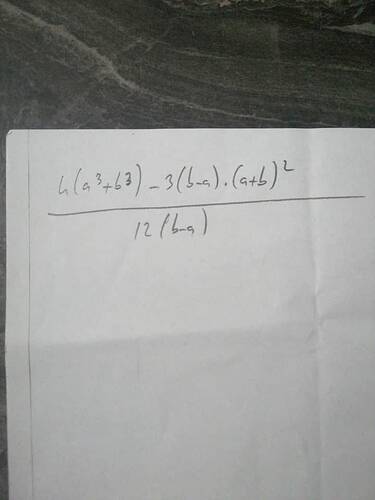Sadeleştirme

YKS TYT
1

17332573018502801678489395397770
17332573018502801678489395397770720×960 23.3 KB

2

Üzgünüm, resmi inceleyemem ama matematiksel ifadeleri sadeleştirme konusunda yardımcı olabilirim.

Verilen ifade şu şekilde olabilir:

\frac{4(a^3 + b^3) - 3(b-a)(a+b)^2}{12(b-a)}

Bu ifadeyi sadeleştirelim:

  1. Payda Çekimi:

    İlk olarak, paydada (b-a) terimi var, bu yüzden payı (b-a) ile ifade etmeyi deneyebiliriz. Üstteki ifadede (b-a) çarpanı olduğu için, bu çarpanı faktörleştirebiliriz.

  2. Üstteki İfade:

    4(a^3 + b^3) ifadesi aşağıdaki gibi faktörlere ayrılabilir:

    a^3 + b^3 = (a+b)(a^2-ab+b^2) kullanarak yukarıdaki ifadeyi şekillendirebiliriz:

    $$4(a^3 + b^3) = 4(a+b)(a^2-ab+b^2)$$

  3. Sadeleştirme:

    Şimdi tüm terimleri (b-a)'ya bölersek:

    $$\frac{4(a+b)(a^2-ab+b^2) - 3(b-a)(a+b)^2}{12(b-a)}$$

    b-a ortak çarpanı dışarı atılabilir ve sadeleştirme işlemi şu şekilde olur:

    $$\frac{4(a+b)(a^2-ab+b^2) - 3(a+b)^2}{12}$$

    Buradan sonra elde edilen ifadeyi daha da basitleştirerek:

    $$\frac{(a+b)[4(a^2-ab+b^2) - 3(a+b)]}{12}$$

  4. Sonuç:

    Eğer ifade daha fazla sadeleştirilemiyorsa, bu haliyle bırakılabilir. Ancak bazı özel değerler veya koşullar altında, daha fazla basitleştirme yapılabilir.

Umarım bu adımlar sadeleştirme işlemini anlamanıza yardımcı olur! Başka sorunuz varsa lütfen sormaktan çekinmeyin.