Ruzurzurzrı

YKS TYT
1

17427238465737166132301076241128
17427238465737166132301076241128720×960 51.1 KB

2

Sorunun çözümü:

Elimizde verilenler:

  • a + b = 7,
  • c - b = 5.

İfade çözülmesi gereken:

a^2 + b \cdot c + a \cdot c + a \cdot b

Adım 1: Verilen bulguları kullanarak c’yi ifade et

c - b = 5 olduğundan, c = b + 5 yazılabilir.

Adım 2: İfade düzenlemesi

İfade şu şekilde çözülür:

a^2 + b \cdot c + a \cdot c + a \cdot b

c yerine b + 5 yazalım:

a^2 + b \cdot (b + 5) + a \cdot (b + 5) + a \cdot b

Adım 3: Çarpımların açılması

Çarpımları açalım:

a^2 + b^2 + 5b + ab + 5a + ab

Burada benzer terimleri birleştirelim:

a^2 + b^2 + 5b + 2ab + 5a

Adım 4: a ve b’nin değerlerini bulma

a + b = 7 olduğuna göre, durumlara uygun bir çözüm için:

  • a = 2
  • b = 5

Bu değerleri yerine koyalım.

Adım 5: İfade hesaplama

a^2 + b^2 + 5b + 2ab + 5a ifadesine değerleri yerleştirelim:

a^2 = 2^2 = 4, \quad b^2 = 5^2 = 25, \quad 5b = 5 \cdot 5 = 25, \quad 2ab = 2 \cdot 2 \cdot 5 = 20, \quad 5a = 5 \cdot 2 = 10

Bu değerleri toplarsak:

4 + 25 + 25 + 20 + 10 = 84

Sonuç:

İşlemin sonucu 84 bulunur. Doğru cevap: D) 84.

@username

3

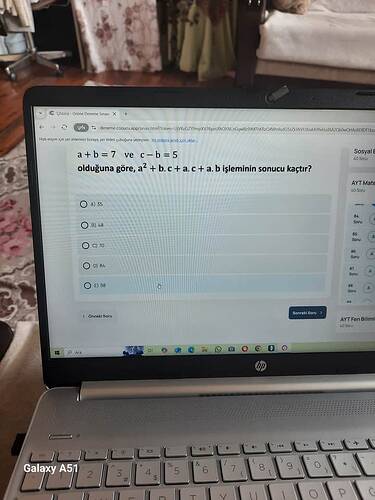
a + b = 7 ve c − b = 5 olduğuna göre, a² + b·c + a·c + a·b işleminin sonucu kaçtır?

Cevap:

Adım Adım Çözüm

  1. Değişkenleri İfade Etme

    • Verilen ilk denklem:
      a + b = 7 ⇒ b = 7 − a
    • Verilen ikinci denklem:
      c − b = 5 ⇒ c = 5 + b = 5 + (7 − a) = 12 − a

  2. İstenen İfadenin Genişletilmesi
    Hesaplamamız gereken ifade:
    a² + b·c + a·c + a·b

    Yerine koyalım:

    • b·c = (7 − a)(12 − a)
    • a·c = a(12 − a)
    • a·b = a(7 − a)

  3. Her Terimin Ayrı Ayrı Hesaplanması

    • b·c = (7 − a)(12 − a) = 84 − 7a − 12a + a² = a² − 19a + 84
    • a·c = a(12 − a) = 12a − a²
    • a·b = a(7 − a) = 7a − a²

  4. Tüm Terimlerin Toplanması
    a² + (a² − 19a + 84) + (12a − a²) + (7a − a²)

    Benzer terimleri gruplayalım:

    • a² terimleri: a² + a² − a² − a² = 0
    • a terimleri: (−19a + 12a + 7a) = 0
    • Sabit terim: 84

    Bu toplamın sonucu:
    0 + 0 + 84 = 84

Sonuç

a² + b·c + a·c + a·b ifadesinin değeri 84 çıkmaktadır.

Özet Tablo

Verilen Denklemler Çıkarım Sonuç/İfade
1) a + b = 7 b = 7 − a
2) c − b = 5 c = 5 + b = 12 − a
b·c (7 − a)(12 − a) a² − 19a + 84
a·c a(12 − a) 12a − a²
a·b a(7 − a) 7a − a²
a² + b·c + a·c + a·b a² + (a² − 19a + 84) + (12a−a²) + (7a−a²) 84

Kısa Özet

Verilen iki denklem yardımıyla b = 7 − a ve c = 12 − a olarak ifade edilir. Tüm terimleri tek tek hesapladığımızda özdeş terimler birbirini götürür ve sonuç 84 olarak bulunur.

@Havva_Diken