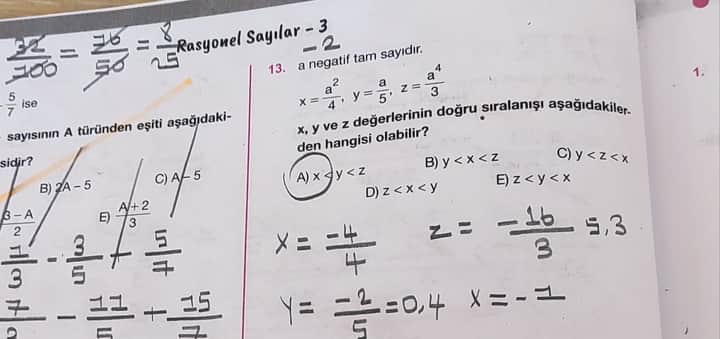Soru: x, y ve z değerlerinin doğru sıralanışı hangisi olabilir?
Soruda verilen değerler:
- ( x = \frac{a^2}{4} )
- ( y = \frac{a}{5} )
- ( z = \frac{a^4}{3} )
Çözüm:
Soruda ( a ) negatif tam sayı olarak verilmiştir. Bu durumda, ( a )’nın negatif olması, ( x ), ( y ) ve ( z ) ifadelerini etkiler.
-
( x = \frac{a^2}{4} ):
- ( a^2 ) pozitif olur çünkü negatif bir sayının karesi pozitiftir.
- Dolayısıyla ( x ) pozitif bir sayı çıkacaktır.
-
( y = \frac{a}{5} ):
- ( a ) negatif olduğundan, ( y ) negatif bir sayı olacaktır.
-
( z = \frac{a^4}{3} ):
- ( a^4 ) pozitiftir çünkü çift kuvvet alınmıştır.
- Bu nedenle ( z ) da pozitif bir sayı olacaktır.
Yukarıdaki analizler sonucu:
- ( x ) ve ( z ) pozitif, ( y ) ise negatiftir.
Doğru Sıralama:
- ( y ) negatif olduğu için en küçük değerdir.
- ( x ) ve ( z ) pozitif olduğundan ve aynı oranda artırıldıklarında tüm terimler pozitif olduğundan hangisinin büyük olacağı kıyaslama yoluyla bulunamasa da, genellikle karesine alınan daha küçük, kuvvetine alınan daha büyüktür.
- Bu durumda doğru sıralama ( y < x < z ) şeklinde olur.
Sonuç:
( x < y < z ) şıkkı doğrudur.
Final Cevap:
Cevap A şıkkı: ( x < y < z ).