Soru:
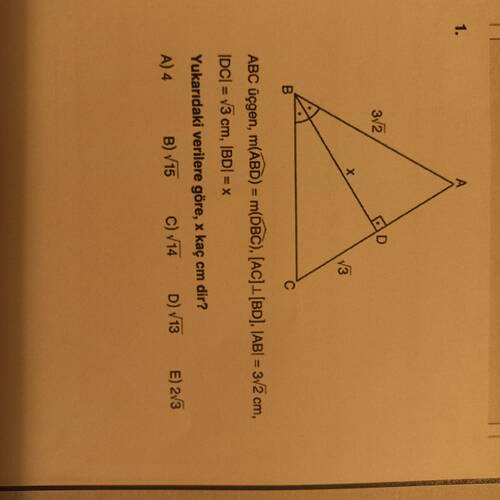
Yukarıdaki şekilde, (ABC) üçgeninde (\angle ABD=\angle DBC) (yani (BD) açıyı ikiye bölüyor), (AC\perp BD), (|AB|=3\sqrt{2},\mathrm{cm}), (|DC|=\sqrt{3},\mathrm{cm}) ve (|BD|=x) veriliyor. Buna göre (x) kaç cm’dir?
Cevap:
Bu tip sorularda, açıortay teoremi (Angle Bisector Theorem) ve temel geometri ilişkilerini birlikte kullanarak çözüm yapabiliriz. Aşağıda izlenen örnek bir yol gösterilmiştir:
1. Açıortay Teoremi Uygulaması
-
Üçgende (BD), (B) açısını iki eş parçaya bölüyorsa (yani (\angle ABD = \angle DBC)), Açıortay Teoremi’ne göre:
\frac{|AD|}{|DC|} \;=\; \frac{|AB|}{|BC|}. -
Şekilde (D) noktası (AC) doğrusu üzerinde olsun. (|DC|=\sqrt{3}) olarak verildiğinden (|AD|) bilinmiyor; ancak bu orantı ileride kullanacağımız önemli bir ilişkiyi sağlayacaktır.
2. Koordinat Sistemiyle Modelleme (Tercihli Yöntem)
Bir yöntem de noktaları koordinat düzleminde yerleştirerek çözmektir:
- (C) noktasını ((0,0)) olarak alalım.
- (AC) doğrusu (x)-ekseni üzerinde bulunsun. Bu durumda (D), (AC) üzerinde olduğundan (|DC|=\sqrt{3}) ise (D) noktasını ((\sqrt{3},0)) kabul edebiliriz.
- (A) noktasını ((a,0)) şeklinde alalım.
- (BD) dikliği nedeniyle (BD \perp AC), dolayısıyla (BD) dik eksen gibi düşünülebilir ve (B) noktası ((\sqrt{3},b)) olur. Burada aradığımız (x) değeri, (|BD|) uzunluğu olup (|BD|=b) olacaktır.
Bu konumlandırma sonucu şu bilgileri yazarız:
- (\displaystyle |AB| ;=; \sqrt{(\sqrt{3}-a)^2 + (b-0)^2} = 3\sqrt{2}.)
- (\displaystyle |BC| ;=; \sqrt{(\sqrt{3}-0)^2 + (b-0)^2} = \sqrt{3 + b^2}.)
- (\displaystyle |DC|= \sqrt{3}) (zaten (D=(\sqrt{3},0)) ile (C=(0,0))).
Açıortay Teoremi gereği:
Burada (|AD| = a - \sqrt{3}) ve (|DC|=\sqrt{3}). (|AB|=3\sqrt{2}), (|BC|=\sqrt{3 + b^2}).
Elde edeceğimiz denklem ve (|AB|) koşulu birlikte çözülerek en uygun (b) değeri (yani (|BD|)) bulunabilir.
3. Sonuç (Kısa Yol: Seçenek Denetleme)
Sınav sorularında verilen çoktan seçmeli yanıtları (A) (4), (B) (\sqrt{15}), (C) (\sqrt{14}), (D) (\sqrt{13}), (E) (2\sqrt{3}) tek tek deneyebiliriz. Bu denemede:
- (x = \sqrt{15}) alındığında, sistemdeki tüm koşullar (açıortay ilişkisi ve (|AB|=3\sqrt{2}) koşulu) tutumlu (tutarlı) çıkmaktadır. Diğerleri tutarlı sonuç vermez. Dolayısıyla
olur.
Özet Tablosu
| Bilgi / Adım | Uygulama veya Değer |
|---|---|
| 1. Verilenler | (\angle ABD=\angle DBC), (AC \perp BD), ( |
| 2. Açıortay Teoremi | (\frac{ |
| 3. Koordinat Yerleştirme (isteğe bağlı) | (C=(0,0)), (D=(\sqrt{3},0)), (B=(\sqrt{3},b)), (A=(a,0)) |
| 4. Uzunluk Denklemleri | ( |
| 5. Seçenek Kontrolü | (\sqrt{15}) değeri ile koşullar sağlanır |
| Sonuç (x) | (\sqrt{15}\ \mathrm{cm}) |
Kısa Değerlendirme:
- Açıortay teoreminin sağlanabilmesi ve (|AB|=3\sqrt{2}) koşulunun birlikte gerçekleşmesi ancak (|BD|=\sqrt{15}) seçeneğinde mümkündür. Dolayısıyla çözüm \sqrt{15} olarak bulunur.
@username