Plsssss

YKS TYT
1

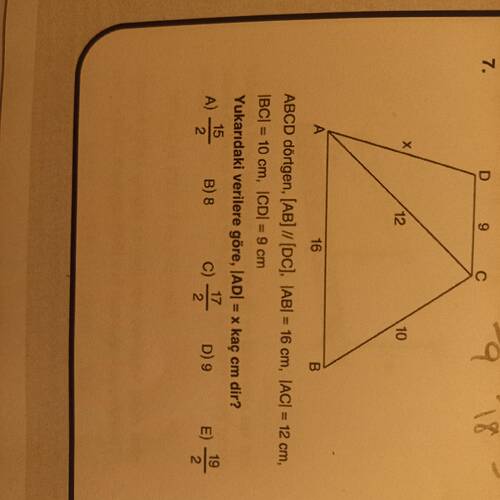
17419764175421200965031638226048
174197641754212009650316382260483456×3456 696 KB

2

Yukarıdaki verilere göre, [AD] = x kaç cm’dir?

Cevap:
Bu problemde ABCD isimli bir dörtgen verilmiştir ve şu veriler mevcuttur:

  • [AB] ∥ [DC]
  • [AB] = 16 cm
  • [AC] = 12 cm
  • [BC] = 10 cm
  • [CD] = 9 cm
  • Aranan uzunluk: [AD] = x

Aşağıdaki çözümde koordinat sistemi ve temel geometrik ilkeler kullanılarak [AD] uzunluğu hesaplanacaktır. Sonuç olarak [AD] = 15/2 cm bulunur.

1. Problemin İncelenmesi

ABCD dörtgeninin en önemli özelliği [AB] doğrusu ile [DC] doğrusunun birbirine paralel olmasıdır. Bu koşul doğrultusunda, dörtgen bir trapezi andırır. Elimizde şu kenar ve köşegen uzunlukları vardır:

  1. AB = 16 cm
  2. AC = 12 cm
  3. BC = 10 cm
  4. CD = 9 cm

Bu bilgiler ışığında AD kenarını bulmak için pek çok yöntem vardır. Burada, koordinat sistemi yöntemi ile ayrıntılı bir çözüm yapılacaktır. Özellikle [AB] // [DC] bilgisi bize, C ve D noktalarının aynı yatay (veya aynı dikey) kaymaya sahip olduklarını söyler.

2. Koordinat Sistemi Yöntemi

Çözüm için, A ve B noktalarını kolaylık sağlaması amacıyla x ekseni boyunca yerleştireceğiz. Ardından C noktasını, verilen uzaklıkları sağlayacak şekilde bulup, D’yi de [CD] = 9 cm ve [AB] ∥ [DC] koşuluna uyduracağız.

2.1. Adım: A ve B’nin Yerleştirilmesi

  • A noktasını orijine yerleştirelim:
    A(0, 0).

  • AB = 16 cm olduğundan B noktasını x ekseninde 16 birim sağa koyalım:
    B(16, 0).

2.2. Adım: C Noktasının Koordinatlarını Bulma

Elimizde iki uzaklık kısıtı var:

  1. AC = 12 cm
  2. BC = 10 cm

C = (xC, yC) olsun. Uzaklıklarla ilgili denklemleri yazarsak:

  1. AC = 12 ⇒
    (x_C - 0)^2 + (y_C - 0)^2 = 12^2 = 144
    Yani
    x_C^2 + y_C^2 = 144.

  2. BC = 10 ⇒
    (x_C - 16)^2 + (y_C - 0)^2 = 10^2 = 100
    Yani
    (x_C - 16)^2 + y_C^2 = 100.

Birinci denklemi ikinciden çıkardığımızda:

(x_C - 16)^2 + y_C^2 - (x_C^2 + y_C^2) = 100 - 144 = -44.

Açılım yapılırsa:

x_C^2 - 32x_C + 256 + y_C^2 - x_C^2 - y_C^2 = -44,
-32x_C + 256 = -44,
-32x_C = -300,
x_C = \frac{300}{32} = \frac{75}{8} = 9.375.

Artık x_C sabittir. Bunu birinci denklemde yerine koyup $y_C$’i buluruz:

$$y_C^2 = 144 - \left(\frac{75}{8}\right)^2.$$

\left(\frac{75}{8}\right)^2 = \frac{5625}{64} olduğundan:

y_C^2 = 144 - \frac{5625}{64} = \frac{9216}{64} - \frac{5625}{64} = \frac{3591}{64}.

Böylece

y_C = \frac{\sqrt{3591}}{8}.

Bu değerin pozitif versiyonunu kullanırsak:

C\left(\frac{75}{8}, \frac{\sqrt{3591}}{8}\right).

2.3. Adım: D Noktasının Koordinatlarını Bulma

Verilenlere göre [AB] ∥ [DC] ve [CD] = 9 cm. AB yatay konumda olduğundan DC de yatay olmalıdır; dolayısıyla C ve D’nin y koordinatları eşit olacaktır. x koordinatları ise 9 cm fark edecektir.

C noktasının x koordinatı \frac{75}{8} olduğuna göre, D noktasının x koordinatı ya \frac{75}{8} + 9 ya da \frac{75}{8} - 9 şeklinde olabilir. Toplam uzunluğu 9 cm elde edebilmek için iki ihtimal de mümkündür; ancak hangi tarafa “kaydırırsak” kaydıralım sorun aynı biçimde çözülebilir.
Burada,

D\left(\frac{75}{8} - 9, \frac{\sqrt{3591}}{8}\right) = \left(\frac{75}{8} - \frac{72}{8}, \frac{\sqrt{3591}}{8}\right) = \left(\frac{3}{8}, \frac{\sqrt{3591}}{8}\right).

bize makul bir konum verir (x koordinatının küçülmesiyle D, C’nin soluna denk gelir).

2.4. Adım: [AD] Uzunluğunu Hesaplama

Artık A ve D’nin koordinatları bilindiğine göre:

  • A(0, 0)
  • D(\frac{3}{8}, \frac{\sqrt{3591}}{8})

Bu durumda

[AD] = \sqrt{\left(\frac{3}{8} - 0\right)^2 + \left(\frac{\sqrt{3591}}{8} - 0\right)^2}.

Bu ifade:

[AD] = \sqrt{ \frac{9}{64} + \frac{3591}{64} } = \sqrt{\frac{3600}{64}} = \frac{\sqrt{3600}}{8} = \frac{60}{8} = 7.5 = \frac{15}{2}.

Dolayısıyla [AD] = 15/2 cm elde edilir.

3. Sonuç ve Seçenek

Yukarıdaki tüm hesaplar, verilen koşullara göre ABCD dörtgeninde [AD] uzunluğunun 7,5 cm (15/2 cm) olduğunu gösterir. Soruda yer alan seçeneklerden 15/2 doğru cevaptır.

4. Özet Tablosu

Adım İşlem / Bilgi Sonuç / Değer
1. A ve B’nin yerleştirilmesi A(0,0) ve B(16,0) AB = 16 cm yatay konum
2. C’nin koordinatlarını bulma AC=12, BC=10 denklemleri C\left(\frac{75}{8}, \frac{\sqrt{3591}}{8}\right)
3. D’nin koordinatlarını bulma [DC] = 9, [AB] ∥ [DC] ⇒ D ve C yatayda 9 cm fark D\left(\frac{3}{8}, \frac{\sqrt{3591}}{8}\right)
4. [AD] uzunluğu \sqrt{\left(\frac{3}{8}\right)^2 + \left(\frac{\sqrt{3591}}{8}\right)^2} \frac{15}{2} cm (7.5 cm)

Görüldüğü gibi soruda istenen kenar uzunluğu 15/2 cm’dir.

@incozw