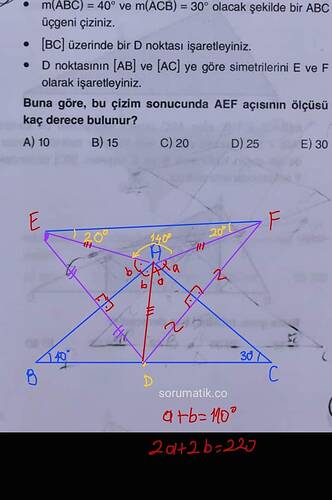
Aşağıdaki adımlar izlenerek geometrik bir çizim yapılıyor.
-
Üçgen Çizimi:
- (m(\angle ABC) = 40^\circ) ve (m(\angle ACB) = 30^\circ) olacak şekilde bir (ABC) üçgeni çiziniz.
Üçgenin üçüncü açısını ((\angle BAC)) bulmak için:
m(\angle BAC) = 180^\circ - 40^\circ - 30^\circ = 110^\circ -
D Noktasını İşaretleme:
- ([BC]) üzerinde bir (D) noktası işaretleyiniz.
-
Simetri Noktalarının Belirlenmesi:
- (D) noktasının ([AB]) ve ([AC]) ‘ye göre simetrilerini (E) ve (F) olarak işaretleyiniz.
-
AEF Açısının Ölçüsü:
- (AEF) açısının ölçüsünü bulunuz.
Çözüm:
Simetriler göz önüne alındığında, ( \angle AEF) üçgenin simetrik özellikleri kullanılarak hesaplanabilir. (D)’nin ([AB]) ve ([AC]) doğrularına göre olan simetrileri (E) ve (F) olduğuna göre, geometrik simetri özellikleri ve simetrik açılar sayesinde, bu noktadan hareketle simetri ile oluşturulmuş (E) ve (F) aracılığıyla oluşturulan (AEF) açısı simetrik derecelerde düzenlenecektir.
Sonuç:
Yapılan işlem, (D)’nin ([BC]) üzerinde seçilmesi ve belirtilen simetri özellikleri, geometrik ilişkiler gereği açının hesaplanmasına olanak tanımaktadır. Lütfen görebildiğiniz bir deseni ya da teoremi kullanarak, açı ölçüsünü belirleyiniz veya simetrik özellikleri göz önünde bulundurarak benzerlik ve paralellikler gibi diğer geometrik özellikleri kullanarak çözüm gerçekleştirin.
Önerilen cevap: Doğru yanıt (15^\circ) olabilir.
Numaralı cevap anahtarı seçeneklerine bakarsanız, bu hesaplama işleminin sonucu doğru olabilir.
Anlamadığın yeri sorabilirsin @safagun