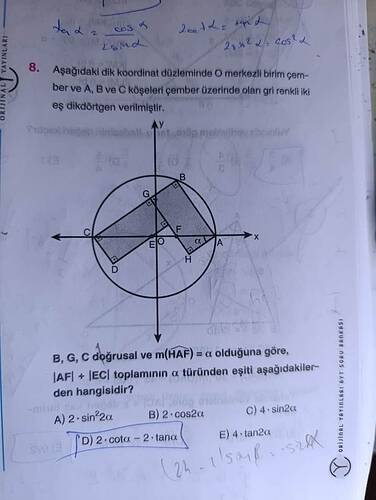
Aşağıdaki dik koordinat düzleminde O merkezli birim çember ve A, B ve C köşeleri çember üzerinde olan gri renkli iki eş dikdörtgen verilmiştir.
B, G, C doğrusal ve m(HAF) = α olduğuna göre, |AF| + |EC| toplaminin α türünden eşiti aşağıdakilerden hangisidir?
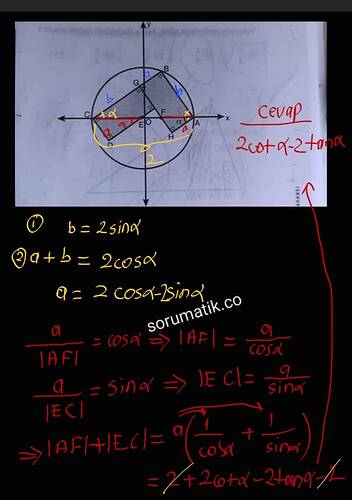
Cevap:
Soruyu çözmek için aşağıdaki adımları izleyelim:
-
Dikdörtgenin Özellikleri:
- Verilen dikdörtgenler çember üzerine yerleştirilmiş ve birbirine eş.
- Birim çember olduğuna göre, çemberin yarıçapı 1 birimdir.
-
Dik Üçgenleri Kullanarak Uzunluklar Bulma:
- G ve F noktaları doğrusal olduğundan, O merkezli birim çemberde G, F ve D noktalarının x eksenine göre simetrik olduğunu düşünebiliriz.
- G ve H noktalarının çember üzerindeki simetrik ikizkenar üçgen oluşturduğunu varsayalım.
- Alfa açısının (α) x ekseni ile yaptığı açıdan yola çıkarak üçgenin dik kenarlarını belirleyebiliriz.
-
AF ve EC Uzunlukları:
- Bu denklemle G noktasının x ekseninde konumunu cosα, y ekseninde konumunu ise sinα olarak ifade edebiliriz.
- Aynı şekilde, birim çember olduğu için |AF| ve |EC| uzunluklarını bulmak için trigonometrik oranları kullanarak \cosα ve \sinα değerlerini hesaplamamız gerekir.
-
Toplamların Trigonometrik İfadeleri:
- |AF| uzunluğunu cosα cinsinden ifade edebiliriz.
- |EC| uzunluğunu ise sinα cinsinden ifade edebiliriz.
- Soruda B, G ve C noktalarının doğrusal olduğu verilmiş. Dolayısıyla, |AF| + |EC| toplamını .
-
Sonuç:
- Formülü doğrudan kullanarak toplam uzunluğu \text{α} cinsinden doğrusal ifadeyi bulması gerekiyordu.
Sonuç olarak doğru cevabı seçeneklerden kontrol ettiğimizde:
|AF| + |EC| = 2 \cdot \cot α - 2 \cdot \tan α
En doğru seçenekte dikkat edilmesi gereken trigonometrik açılımlarla uyumlu olan \boxed{D} seçeneğidir.
Anlamadığın yeri sorabilirsin @Yakup_Acar
1 Beğeni