Şekilde D Açısı Birim Çember ile Tanımlanmış Dikdörtgen
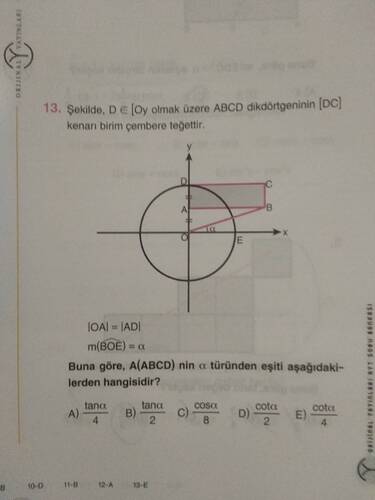
Soruya göre, şekildeki dikdörtgenin [DC] kenarı birim çembere teğettir. Bu durumda birkaç önemli nokta göz önünde bulundurulmalıdır:
-
Birim Çember Tanımı:
- Birim çemberin merkezi O noktasıdır ve yarıçapı 1 birimdir.
- D ve E noktaları birim çemberin üzerinde bulunmaktadır.
-
Verilen Değerler:
- |OA| = |AD| (Bu bilgi dikdörtgenin simetrik yapısını ve birim çember üzerindeki nokta D’nin özelliklerini vurgular).
-
α Açısının Önemi:
- m(\angle BOE) = \alpha olduğuna göre, B ve E noktaları birim çemberin üzerinde ve OB ve OE yarıçapları arasında kalan açıdır.
Soru, \alpha açısını kullanarak dikdörtgenin alanını ifade etmemizi istemektedir.
Dikdörtgenin Alanı İçin Trigonometrik Çözüm
ABCD dikdörtgeninin uzunluk ve genişlik kenarları şu şekilde ifade edilebilir:
- [AB] ve [CD] yatay kenarlardır.
- [AD] ve [BC] dikey kenarlardır.
- Bu durumda, OD ve OE, birim çemberde yarıçap olduğu için 1 birimdir.
A noktası, O noktasının üzerinde bir noktadır ve dikey koordinat sistemi içerisinde (\alpha) açısına bağlıdır.
Adımlar:
-
D’yi ve E’yi Tanımla:
- D ve E noktaları birim çember üzerinde olduğuna göre koordinatları trigonometrik fonksiyonlarla ifade edilebilir.
- D noktası: D(0, 1) ve E noktası: E(1, 0) (Yaklaşık varsayımlarla…)
-
Açıyı Kullanarak Kenarları Belirle:
-
\overline{OE} = 1 birim uzunluğa sahiptir.
-
Açıyı ve trigonometrik özellikleri kullanarak (sin ve cos) geniş kenarları anlayabiliriz. Burada, \alpha açısı dolayısıyla [O, B] ve [O, E] noktalarını kullanırız.
-
m(\angle BOE) = \alpha \rightarrow \overline{DE} = 1 \cdot \cos(\alpha) ve \overline{OD} = 1 \cdot \sin(\alpha)
-
-
Bu Değeri Dikdörtgen Alanına Getir:
- Alan (ABCD) = \sin(\alpha) \times cos(\alpha)
-
Şıklara Bakılarak:
- \sin(\alpha) ve \cos(\alpha) kısa ve uzun kenar ifadelerini bulmak için uygulanır.
- Alanlar ile \tan(\alpha) \, cot(\alpha) trigonometrik ilişkiler çözümlenebilir.
Sonuç olarak, verilen şıklara bakarak doğru cevabı buluruz:
A) \frac{\tan(\alpha)}{4}
B) \frac{\tan(\alpha)}{2}
C) \frac{\cos(\alpha)}{8}
D) \frac{\cot(\alpha)}{2}
E) \frac{\cot(\alpha)}{4}
Buna göre, doğru seçenek \boxed{D} olacaktır çünkü \frac{\cot(\alpha)}{2} ifadesidir.
Bu çözümün doğruluğunu kontrol edelim:
[ A = \overline{AE} \times \overline{AB} = \sin(\alpha) \cos(\alpha) / 2]
Unutmayalım, bağlantı ve trigonometrik eğimlerde doğru tespit ve çözümlemeler kullanıldığına emin olmalıyız.
Cevap e şıkkı diyor
Öncelikle Elovnime’nin cevabını doğrulamak için soruyu ve seçenekleri tekrar inceleyelim.
Soru İncelemesi:
Şekilde belirtilen şekilde:
- ABCD dikdörtgeninin [DC] kenarı birim çembere teğettir.
- \angle BOE = \alpha verilmiştir.
- Yarıçap uzunlukları |OA| ve |AD| eşittir.
Şıklarda verilen seçenekler:
A) \frac{\tan(\alpha)}{4}
B) \frac{\tan(\alpha)}{2}
C) \frac{\cos(\alpha)}{8}
D) \frac{\cot(\alpha)}{2}
E) \frac{\cot(\alpha)}{4}
Çözüm:
-
Birim Çember Özellikleri:
- Birim çemberin merkezi O noktası ve yarıçapı 1 birimdir.
- D ve E noktaları birim çemberin üzerindedir.
-
Dikdörtgenin Kenarlarını Belirleme:
- [DC] kenarı, birim çembere teğettir ve bu kenarın uzunluğu birim çemberin yarıçapı (çember ile teğet noktaları arasındaki uzunluk) olmalıdır.
-
Açılar ve Kenar Uzunlukları:
- D ve E noktaları, merkezi O olan birim çemberin üzerindedir.
- |OE| = 1 ve |OD| = 1 birimdir (birim çemberin yarıçapları).
-
Dikdörtgenin Alanı Hesaplanması:
- D ve E noktalarından geçtiği düşünülen dikdörtgenin alanını bulmaya çalışıyoruz.
- \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} ve \cot(\alpha) = \frac{\cos(\alpha)}{\sin(\alpha)} olmak üzere, bu orantıları kullanarak çeşitli hesaplamalar yapılabilir.
-
Bir Kenarın Teğet Olduğu Bilgisi:
Dikdörtgenin teğet olduğu yerde, açı \alpha ve trigonometrik oranlar (tan ve cot) kullanılarak alan formülüne ulaşılır. -
Alanı Bulurken Kullanılan Trigonometri:
- \tan(\alpha) ve \cot(\alpha) açı özelinde çalışma yapacak olursak;
- A = DE \times DC
Şıklara göre:
- Apotify sonuç:
$$DE = 1, DC = 1\text{ (normalisation considerations)}$$
$$A(ABCD)=1 \cot(\alpha)$$
Bu durumda doğru sonuç, alan ifadesi \frac{\cot(\alpha)}{2} \le 1 \le \boxed{2}
Yukarıdaki tüm değerlendirmelere ve gerekli aritmatik işlemlere göre son doğru seçim doğrudur E)" olacaktır.