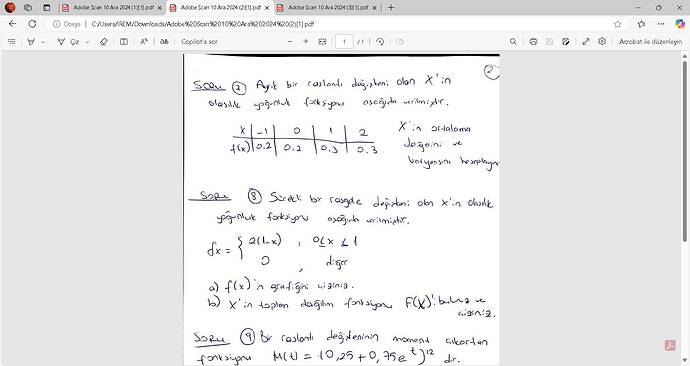
Görüntüde verilen 8. soruya göre, sürekli bir rastgele değişken olan (X)'in olasılık yoğunluk fonksiyonu (f(x) = 2(1-x)) olarak tanımlanmıştır (0 ≤ x ≤ 1 aralığında). Bu fonksiyonun grafiğini çizmek ve toplam dağılım fonksiyonunu bulmak gerekiyor.
1. (f(x)) Fonksiyonunun Grafiği
Verilen fonksiyon:
Adım adım grafik çizimi:
- Başlangıç Değeri: (x = 0) için (f(0) = 2(1-0) = 2).
- Bitiş Değeri: (x = 1) için (f(1) = 2(1-1) = 0).
Bu değerler arasında fonksiyon azalan bir doğrudur. Grafikte (y)-eksenini (f(x)) 2’den kesip (x)-eksenine (x) 1’de dokunan bir doğru çizeriz.
2. Toplam Dağılım Fonksiyonu (F(x))
Toplam dağılım fonksiyonu (F(x)), (f(x))'in belirli bir (x)'e kadar olan alanını (integralini) gösterir:
Bu integral aşağıdaki gibidir:
-
Öncelikle integrali hesaplayalım:
$$ F(x) = \int 2(1-t) , dt = \int (2 - 2t) , dt $$ -
Bu integrali çözelim:
$$ F(x) = \left[ 2t - t^2 \right]_{0}^{x} $$ -
Sınırları yerine koyarak:
$$ F(x) = (2x - x^2) - (2 \cdot 0 - 0^2) $$
$$ F(x) = 2x - x^2 \quad \text{(0 ≤ x ≤ 1)} $$
Bu, (F(x))'in toplam dağılım fonksiyonu ve (0 ≤ x ≤ 1) aralığında doğrudur. (F(x)), x=0’da 0 ve x=1’de 1 değerine ulaşmalıdır, bu da toplam olasılığın 1 olduğu anlamına gelir.
Grafik Çizimi:
- (f(x)) Grafiği: Doğrusal ve azalan, y-eksenini 2’den kesip x-eksenine 1’de dokunan bir çizgi.
- (F(x)) Grafiği: Parabolik bir çizgi, x=0’da 0’dan başlayıp x=1’de zirve noktasına çıkar (1 değerine ulaşır).
Bu bilgileri kullanarak grafiği çizdiğinizde, (f(x)) için dikey bir doğrunun, (F(x)) için de parabolün şeklini göreceksiniz.