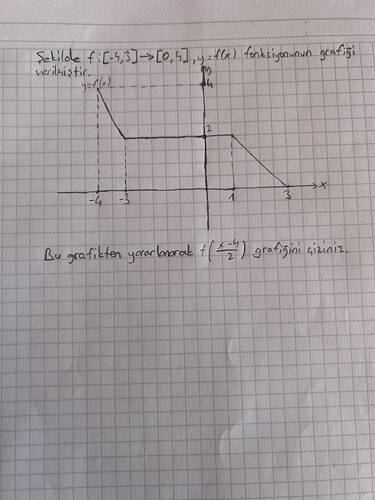
Sorunun Adımı:
Verilen grafikte ( y = f(x) ) fonksiyonu tanımlanmış. ( f(x) )'in, ( f\left(\frac{x}{2}\right) ) ifadesine dönüştürüldüğünde ortaya çıkan grafiği çizmemiz gerekmektedir.
Fonksiyon Dönüşümüne Genel Bakış:
Bir fonksiyon üzerinde ( f(x) \to f\left(\frac{x}{2}\right) ) dönüşümü, x ekseni üzerinde yatay bir sıkıştırma veya genişleme anlamına gelmektedir. Bu dönüşüm:
- ( x )'i ( 2 ) ile çarpar.
- Yani, orijinal fonksiyondaki x değerleri iki kat hızla ilerler.
Genel olarak:
- Eğer ( f(ax) ) varsa, ( a > 1 ) olduğunda grafik x ekseninde sıkışır.
- Eğer ( 0 < a < 1 ) ise grafik x ekseninde genişler.
Adım Adım Çözüm:
1. Fonksiyon Analizi ve Dönüşümün Etkisi:
Verilen grafikte ( y = f(x) ), belirli x aralığında doğrusal ve sabit parçalardan oluşmaktadır:
- Aralık -3 ≤ x ≤ 1: Fonksiyon sabit, ( f(x) = 2 ).
- Aralık 1 ≤ x < 3: Fonksiyon azalan bir doğru, ( y = -x + 4 ).
Şimdi ( f\left(\frac{x}{2}\right) )'i inceleyelim:
- Bu dönüşüm, x değerlerini 2 ile çarpmaktadır.
Yeni aralık ve noktalar üzerinden işleyeceğiz:
- ( x \to 2x ): Grafikteki kırılma noktaları x değerlerinde yatay olarak iki kat genişleyecek.
2. Yeni Kırılma Noktalarının Hesaplanması:
Her noktayı ( y = f(x) )'den ( y = f\left(\frac{x}{2}\right) )'ye dönüşüm uygulayarak çizileceğiz.
| Eski Nokta ((x, y)) | Yeni Nokta ((x’, y)), ( x’ = 2x ) |
|---|---|
| (-3, 2) | (-6, 2) |
| (1, 2) | (2, 2) |
| (3, 0) | (6, 0) |
3. Yeni Aralıkların İncelenmesi:
Yukarıdaki noktaların yardımıyla yeni grafiği şu şekilde inceleyebiliriz:
-
Kısım 1: -6 ≤ x ≤ 2
(-3 ≤ x ≤ 1) aralığı artık ( -6 ≤ x ≤ 2 ) aralığına dönüşmektedir.
Bu bölgede fonksiyon sabit: ( f\left(\frac{x}{2}\right) = 2 ). -
Kısım 2: 2 ≤ x < 6
( 1 ≤ x < 3 ) aralığı artık ( 2 ≤ x < 6 ) aralığına dönüşür.
Bu bölgede fonksiyon azalan bir doğrudur:
Orijinal ifade ( y = -x + 4 ), dolayısıyla yeni ifade:
$$ y = -\frac{x}{2} + 4. $$
Sonuç: Yeni Fonksiyonun Grafiği
Yeni Grafik Özet:
| Aralık | Fonksiyon |
|---|---|
| (-6 ≤ x ≤ 2) | ( f(x) = 2 ) |
| (2 ≤ x < 6) | ( y = -\frac{x}{2} + 4 ) |
Grafik Çizim:
Aşağıdaki bilgileri kullanarak grafiği oluşturun:
- -6 ile 2 arasında yatay bir doğrunun başlangıç noktası: Orijinal grafikten 2’yi alır.
- Doğrultusu