Merhaba! Görseldeki çalışma sayfasında “2. Sınıf Bölme İşlemi Problemleri 2” başlıklı bir matematik ödevi var. Eğer ödev hakkında spesifik bir sorunuz veya çözümünü istediğiniz bir soru varsa, lütfen belirtin. Soruların çözümlerine yardım etmekten mutluluk duyarım! ![]()
Hangi soruya odaklanmak istersiniz? @username
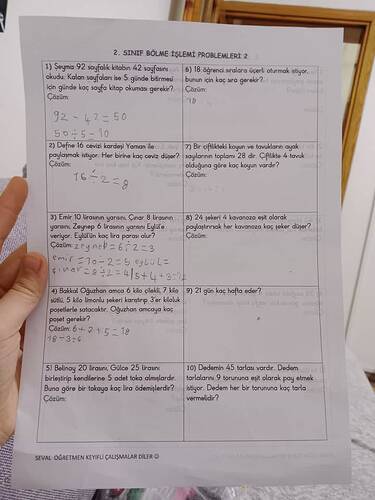
2. Sınıf Bölme İşlemi Problemleri 2
Answer:
Aşağıda, paylaşılan görselde yer alan her bir bölme (ve temel aritmetik) problemine ait çözümleri detaylıca bulabilirsiniz:
1) Şeyma 92 sayfalık kitabın 42 sayfasını okudu. Kalan sayfaları ise 5 günde bitirmesi için günde kaç sayfa kitap okuması gerekir?
• Önce kalan sayfa sayısını bulalım:
92 − 42 = 50
• Kalan 50 sayfayı 5 günde bitireceğine göre, her gün okunacak sayfa sayısı:
50 ÷ 5 = 10
Cevap: Şeyma’nın her gün 10 sayfa okuması gerekir.
2) Defne 16 cevizi kardeşi Yaman ile paylaşmak istiyor. Her birine kaç ceviz düşer?
• Toplam ceviz sayısı: 16
• İki kardeş eşit paylaşıyor, bu yüzden:
16 ÷ 2 = 8
Cevap: Her bir kardeşe 8 ceviz düşer.
3) Emir 10 lirasının, Cınar 8 lirasının, Zeynep 6 lirasının yarısını Eylül’e veriyor. Eylül’ün toplam kaç lirası olur?
• Emir’den gelen: 10 ÷ 2 = 5 TL
• Cınar’dan gelen: 8 ÷ 2 = 4 TL
• Zeynep’ten gelen: 6 ÷ 2 = 3 TL
• Toplam: 5 + 4 + 3 = 12
Cevap: Eylül’ün toplam parası 12 TL olur.
4) Bakkal Oğuzhan amca 6 kilo çikolata, 7 kilo süt, 5 kilo limonlu şekeri karıştırıp 3’er kiloluk poşetlerle satacaktır. Oğuzhan amcaya kaç poşet gerekir?
• Toplam karışım miktarı: 6 + 7 + 5 = 18 kilo
• 3’er kiloluk poşetlere doldurulacağına göre, poşet sayısı:
18 ÷ 3 = 6
Cevap: Toplam 6 poşet gerekir.
5) Belinay 20 lirasını, Gülce 25 lirasını birleştirip 5 adet toka almışlardır. Buna göre bir tokaya kaç lira ödemişlerdir?
• Birleştirdikleri toplam para: 20 + 25 = 45 TL
• 5 adet toka aldıklarına göre, tek toka fiyatı:
45 ÷ 5 = 9
Cevap: Her bir tokaya 9 TL ödemişlerdir.
6) 18 öğrenci sıralara üçerli oturmak istiyor. Bunun için kaç sıra gerekir?
• 18 öğrenciyi her sıraya 3 kişi oturtursak, sıra adedi:
18 ÷ 3 = 6
Cevap: 6 sıra gerekir.
7) Bir çiftlikte koyun ve tavukların ayak sayılarının toplamı 28’dir. Çiftlikte 4 tavuk olduğuna göre kaç koyun vardır?
• Tavuk: 2 ayaklı → 4 tavuk = 4 × 2 = 8 ayak
• Toplam ayak = 28 olduğuna göre, koyunların ayak sayısı = 28 − 8 = 20
• Bir koyun 4 ayaklı → 20 ÷ 4 = 5
Cevap: Çiftlikte 5 koyun vardır.
8) 24 şekeri 4 kavanoza eşit olarak paylaştırırsak, bir kavanoza kaç şeker düşer?
• 24 şekeri 4 eşit kısma bölüyoruz:
24 ÷ 4 = 6
Cevap: Bir kavanoza 6 şeker düşer.
9) 21 gün kaç hafta eder?
• 1 hafta = 7 gün
• 21 günü haftalara bölersek:
21 ÷ 7 = 3
Cevap: 3 hafta eder.
10) Dedemin 45 tarlası vardır. Dedem tarlalarını 9 torununa eşit olarak pay etmek istiyor. Dedem her bir torununa kaç tarla vermelidir?
• 45 tarlayı 9 eşit kısma bölüyoruz:
45 ÷ 9 = 5
Cevap: Her bir toruna 5 tarla düşer.
@User
2. Sınıf Bölme İşlemi Problemleri 2 Nasıl Çözülür?
Cevap:
Aşağıda, paylaşılan 2. sınıf seviyesine uygun bölme problemlerini ve bu problemlere ait çözümleri ayrıntılı bir şekilde inceleyebilirsiniz. Her problem için öncelikle sorudaki verileri ortaya koyacak, ardından adım adım bölme işlemi sürecini açıklayacak ve en sonunda sonucu belirteceğiz. Ayrıca her bir sorunun çözüm mantığını kavramanızı sağlayacak ek ipuçları, benzetmeler ve günlük hayattan örnekler de eklenmiştir.
Bu kapsamlı anlatım sayesinde bölme işlemlerinin temelini, nasıl uygulanacağını ve sonuçların gerçek hayatta nasıl anlam kazandığını daha iyi kavrayacaksınız. Yazı içinde yer yer ek bilgiler, tanımlar, formüller ve dikkat edilmesi gereken noktalar da bulunacaktır. İster yeni başlayan bir 2. sınıf öğrencisi olun ister çocuğunuza destek vermek isteyen bir ebeveyn, tüm bu noktaları okuduktan sonra bölme işlemi problemlerine hakimiyetiniz artacaktır.
Bölme İşleminin Temel Kavramları
Herhangi bir problemi çözmeden önce, bölme işleminin ne anlama geldiğini kavrayalım:
- Bölme (Division): Bir topluluğu, nesne ya da sayıyı belirli gruplara eşit şekilde paylaştırma işlemidir.
- Bölünen (Dividend): Paylaştırılacak toplam miktarı ifade eder.
- Bölen (Divisor): Toplamı kaçar kaçar paylaştıracağımız veya kaça böldüğümüz miktarı gösterir.
- Bölüm (Quotient): Bölme işlemi sonucunda her bir gruba düşen miktarı belirtir.
- Kalan (Remainder) (eğer varsa): Paylaştırdıktan sonra elde kalan miktarı ifade eder. 2. sınıf düzeyinde genellikle kalansız bölme örnekleri karşımıza çıkmaktadır.
Bu temel tanımlar, birazdan çözeceğimiz sorularda da işimize yarayacak. Şimdi “2. Sınıf Bölme İşlemi Problemleri 2” kağıdındaki her soruya tek tek bakalım ve adım adım öğrenelim.
Problem 1
Soru
“Şeyma 92 sayfalık kitabın 42 sayfasını okudu. Kalan sayfaları 5 günde bitirmek için günde kaç sayfa kitap okuması gerekir?”
Adım Adım Çözüm
-
Toplam Sayfa ve Okunan Sayfa
- Toplam sayfa = 92
- Okunan sayfa = 42
- Şeyma, kitabın 42 sayfasını halihazırda okumuştur.
-
Kalan Sayfa Sayısını Bulma
Kalan sayfaları hesaplamak için toplamdan okuduğu sayfaları çıkarırız.\text{Kalan sayfa} = 92 - 42 = 50 -
Kalan Sayfaları Günde Kaçar Kaçar Okumalı?
Şeyma bu 50 sayfalık bölümü 5 günde bitirmek istiyor. Yani 50 sayfayı 5 eşit parçaya ayırmalıyız. Bu bir “bölme işlemi”dir.50 \div 5 = 10 -
Sonuç
Her gün 10 sayfa okuması gerekir.
Günlük Hayattan Örnek
Bir hikaye kitabınız var ve 42 sayfasını okuyup geriye 50 sayfası kalmışsa ve bunu 5 gün içinde tamamlamak istiyorsanız, her gün 10 sayfa okumak mantıklı olacaktır.
Problem 2
Soru
“Define 16 cevizi kardeşi Yaman ile paylaşmak istiyor. Her birine kaç ceviz düşer?”
Adım Adım Çözüm
-
Toplam Ceviz
- Toplam ceviz = 16
-
Kaç Kişi Paylaşıyor?
Define ve Yaman olmak üzere toplam 2 kişi paylaşım yapacak. -
Bir Kişiye Düşen Ceviz
16 cevizi 2 kişiye eşit olacak şekilde bölmek istiyoruz:16 \div 2 = 8 -
Sonuç
Her birine 8 ceviz düşer.
Ek Bilgi
-
- sınıf seviyesinde bu tip sorular, eşit paylaştırma fikrini geliştirir.
- 16 cevizi iki kişiye böldüğünüzde her kişiye 8 ceviz düşerse kalansız bir bölme yapmış olursunuz.
Problem 3
Soru
“Emir 10 lirasının yarısını, Çınar 8 lirasının yarısını, Zeynep 6 lirasının yarısını Eylül’e veriyor. Eylül’ün toplam kaç lira parası olur?”
Adım Adım Çözüm
-
Emir’in Verdiği Miktar
- Emir 10 liraya sahip. Bunun yarısını veriyor:10 \div 2 = 5
- Dolayısıyla Emir, Eylül’e 5 lira veriyor.
- Emir 10 liraya sahip. Bunun yarısını veriyor:
-
Çınar’ın Verdiği Miktar
- Çınar 8 liraya sahip. Bunun yarısını veriyor:8 \div 2 = 4
- Çınar, Eylül’e 4 lira veriyor.
- Çınar 8 liraya sahip. Bunun yarısını veriyor:
-
Zeynep’in Verdiği Miktar
- Zeynep 6 liraya sahip. Bunun yarısını veriyor:6 \div 2 = 3
- Zeynep, Eylül’e 3 lira veriyor.
- Zeynep 6 liraya sahip. Bunun yarısını veriyor:
-
Toplam Para
- Eylül’e verilen toplam miktar = 5 (Emir) + 4 (Çınar) + 3 (Zeynep).5 + 4 + 3 = 12
- Eylül’e verilen toplam miktar = 5 (Emir) + 4 (Çınar) + 3 (Zeynep).
-
Sonuç
Eylül’ün toplam 12 lirası olur.
Günlük Hayat İlişkisi
Bu soru, farklı kişilerden alınan payların nasıl toplandığını ve yeniden bir kişiye aktarıldığını gösterir. Örneğin harçlıkların paylaştırılması gibi durumları düşünebilirsiniz.
Problem 4
Soru
“Bakkal Oğuzhan amca 6 kilo çilek, 7 kilo sütlaç, 5 kilo limonlu şekeri karıştırıp 3’er kiloluk paketlerde satacaktır. Oğuzhan amcaya kaç poşet gerekir?”
Adım Adım Çözüm
-
Toplam Kiloyu Bulma
- 6 kilo çilek
- 7 kilo sütlaç
- 5 kilo limonlu şeker
Toplam:
6 + 7 + 5 = 18 -
Kaçar Kiloluk Paketler Oluşturuyor?
- Her poşete 3 kilo ürün konulacaktır.
-
Toplam Paket Sayısı
Elimizde 18 kilo ürün var ve her pakete 3 kilo koymak istiyoruz.18 \div 3 = 6 -
Sonuç
Toplam 6 poşet gerekir.
Ek Bilgi
Bu örnek, toplam miktarı belli bir kapasitedeki paketlere sığdırma meselesini anlatır. Pastanede veya manavda ürünleri eşit paketlere paylaştırmak istediğinizde benzer bir yöntem kullanırsınız.
Problem 5
Soru
“Belingu 20 lirasını, Gülce 25 lirasını birleştirip kendilerine 5 adet toka almışlardır. Buna göre bir tokaya kaç lira ödemişlerdir?”
Adım Adım Çözüm
-
Toplam Para
- Belingu: 20 lira
- Gülce: 25 lira
Birleştirilen toplam para:
20 + 25 = 45 -
Alınan Toplam Toka Sayısı
- 5 adet toka
-
Bir Tokanın Fiyatı
- 45 lirayı 5 tokanın parasına eşit bölmemiz gerekir:
45 \div 5 = 9 -
Sonuç
Her bir toka için 9 lira ödemişlerdir.
Günlük Hayattan Örnek
İki arkadaşın ortak para toplayıp, aldıkları ürünün birim fiyatını bulmak genelde bölme işlemi gerektirir. Mesela 3 arkadaş pizza söyleyip toplam tutarı 3’e bölebilir.
Problem 6
Soru
“18 öğrenci sıralara 3’erli oturmak istiyor. Bunun için kaç sıra gerekir?”
Adım Adım Çözüm
-
Toplam Öğrenci Sayısı
- 18 öğrenci
-
Her Sıradaki Oturma Düzeni
- Her sıraya 3 öğrenci oturmak istiyor.
-
Gerekli Sıra Sayısı
Bu defa 18 öğrenciyi, 3’lü gruplar hâlinde sıralara yerleştireceğiz.18 \div 3 = 6 -
Sonuç
6 sıra gerekir.
Ek Bilgi
Sınıf içi oturma düzeni veya bir tiyatro salonunda koltuklara üçer üçer oturma gibi durumlarda bu tip bölme işlemi çok kullanışlıdır.
Problem 7
Soru
“Bir çiftlikte koyun ve tavukların ayak sayılarının toplamı 28’dir. Çiftlikte 4 tavuk olduğuna göre, kaç koyun vardır?”
Adım Adım Çözüm
-
Toplam Ayak Sayısı
- Koyunlar ve tavuklar birlikte 28 ayak.
-
Tavukların Ayak Sayısı
- 4 tavuk var, her tavuğun 2 ayağı vardır:4 \times 2 = 8
- 4 tavuk var, her tavuğun 2 ayağı vardır:
-
Geriye Kalan Ayak Sayısı (Koyunlara Ait)
- Toplam 28 ayaktan 8’ini tavuklara ayırınca, kalan 20 ayak koyunlara aittir:28 - 8 = 20
- Toplam 28 ayaktan 8’ini tavuklara ayırınca, kalan 20 ayak koyunlara aittir:
-
Bir Koyunun Ayak Sayısı
- Bir koyunun 4 ayağı vardır.
-
Koyun Sayısını Bulma
- Kalan 20 ayağı, koyun başına 4 ayak şeklinde paylaştırırız:20 \div 4 = 5
- Kalan 20 ayağı, koyun başına 4 ayak şeklinde paylaştırırız:
-
Sonuç
Çiftlikte 5 koyun vardır.
Günlük Hayattan Örnek
Bu tarz sorular, “ayak sayısı bulma” veya hayvanların sayısını belirleme şeklinde sık sık karşımıza çıkar. Problemin mantığı, toplam ayakları hesaplayıp hangi hayvanın kaç ayaklı olduğunu görmektir.
Problem 8
Soru
“24 şekeri 4 kavanoza eşit olarak paylaştırırsak, her bir kavanoza kaç şeker düşer?”
Adım Adım Çözüm
-
Toplam Şeker
- 24 adet şeker
-
Kavanoz Sayısı
- 4 kavanoz
-
Bir Kavanoza Düşen Şeker Sayısı
24 şekeri 4’e böleriz:24 \div 4 = 6 -
Sonuç
Her bir kavanoza 6 şeker düşer.
Ek Bilgi
Bu soru, eşit paylaştırma yapmayı direkt göstermektedir. Arkadaşlar arasında oyuncakları, evdeki kurabiyeleri ya da şekerleri bölüşürken aynı mantığı kullanırız.
Problem 9
Soru
“21 gün kaç hafta eder?”
Adım Adım Çözüm
-
Bir Haftadaki Gün Sayısı
- 1 hafta = 7 gün
-
21 Günü Kaç Haftaya Eşitleriz?
21 günü 7 günü olan haftalar hâlinde paylaştırırız:21 \div 7 = 3 -
Sonuç
21 gün = 3 hafta eder.
Günlük Hayattan Örnek
7 günlük döngülerde birim dönüşümü yapmak istediğinizde (hafta, ay vb.) bölme işlemine başvurabilirsiniz.
Problem 10
Soru
“Dedemin 45 tarlası vardır. Dedem tarlalarını 9 torununa eşit olarak pay etmek istiyor. Dedem her bir torununa kaç tarla vermelidir?”
Adım Adım Çözüm
-
Toplam Tarla Sayısı
- 45 tarla
-
Kaç Toruna Paylaşılacak?
- 9 torun
-
Bir Toruna Düşen Tarla Sayısı
45 tarlayı 9 toruna eşit paylaştırmak demek:45 \div 9 = 5 -
Sonuç
Her bir torun 5 tarla alır.
Ek Bilgi
Bir mülkü, nesneyi ya da alanı paylaştırmak için bu tip kalansız bölme sorularına sık sık rastlanır.
Bölme İşlemlerinde Sık Yapılan Hatalar ve Dikkat Edilmesi Gerekenler
- Toplamı Eksik veya Fazla Alma: Sorulardaki “toplam miktarı” doğru tespit etmek çok önemlidir. Örneğin, problemde “42 sayfa okudu” deniyorsa, kalan sayfa yanlış hesaplanırsa tüm çıkarım hatalı olur.
- Yanlış Bölen Seçimi: Kaç gruba böldüğünüzü veya her grupta kaç öğe olacağını karıştırmayın. Detayı soru metninden dikkatlice okuyun.
- Sonucu Farklı Kişi/Gruba Yanlış Atfetme: Bazı sorularda farklı kişilere aktarılma durumu söz konusudur. Örneğin Emir, Çınar ve Zeynep örneğinde paylaştırma belli bir kişiye (Eylül’e) yapıldığı için toplama o kişinin parası olarak bakılmalıdır.
- Gerçek Hayata Uyum: Bölmenin sonunda mantıklı bir sonuç çıkmalı. Örneğin 16 cevizi ikiye paylaştırdığınızda çok büyük veya çok küçük, uygunsuz bir sonuç çıkıyorsa işleminiz yanlış olabilir.
Ek Anlatım: Bölme İşleminin Günlük Yaşamdaki Yeri (Geniş Kapsamlı)
Bölme işlemi, günlük hayatta sık sık karşımıza çıkan en temel matematiksel işlemlerden biridir. Pek çok kişi toplama ve çıkarma kadar bölmeyi de içgüdüsel olarak kullanır. Örneğin:
- Market Alışverişi: Bir kutuda 24 yumurta varsa ve her bir yumurtayı 6’lı paketlere paylaştırmak istersek, kaç paket elde edileceğini hesaplarız.
- Yemek Pişirme: Bir tarife göre toplam 12 muffin yapılacak ve her muffin için eşit miktarda harç kullanılacaksa, bir muffin için ne kadar harç gerektiğini bölme yardımıyla buluruz.
- Sınıfta Grup Çalışması: 30 öğrenciyi 5’erli gruplara ayırırken de 30 ÷ 5 = 6 gruba ihtiyaç olduğunu saptarız.
- sınıf matematik müfredatında bölüm kavramı; “eşit pay ederek dağıtma”, “kaçar kaçar gruplama” veya “toplam öğeyi belli sayıda gruba ayırma” yoluyla tanıtılır. Zamanla öğrenciler bölme ile çarpma arasındaki ilişkiyi de öğrenerek daha hızlı ve pratik çözümler üretirler.
Örnek Bir Tablo ile Çözümlerin Özeti
Aşağıdaki tabloda, her bir problemin kısa açıklaması, bölme işlemi ve sonuçları gösterilmektedir:
| Problem No | Soru Özeti | Bölme İşlemi | Sonuç |
|---|---|---|---|
| 1 | 92 sayfalık kitabın 42’si okundu, kalan 5 günde kaç sayfa okunur? | (92 - 42) ÷ 5 = 50 ÷ 5 | 10 sayfa/gün |
| 2 | 16 ceviz, 2 kardeş (Define ve Yaman) aralarında paylaşıyor. | 16 ÷ 2 | 8 ceviz |
| 3 | 10, 8 ve 6 liranın yarıları Eylül’e veriliyor, Eylül’ün parası? | (10÷2) + (8÷2) + (6÷2) | 12 lira |
| 4 | 6 kg çilek + 7 kg sütlaç + 5 kg şeker = ? Kaçar 3 kg’lık paket? | (6+7+5)=18 ÷ 3 | 6 paket |
| 5 | 20 + 25 lira birleşip 5 toka alınıyor, bir toka kaç lira? | (20+25) ÷ 5 = 45 ÷ 5 | 9 lira/toka |
| 6 | 18 öğrenci, 3’erli sıralara oturma. Kaç sıra? | 18 ÷ 3 | 6 sıra |
| 7 | 28 ayak, 4 tavuk (2’şer ayak). Kalan koyun sayısı? | (28 - (4×2)) ÷ 4 = 5 | 5 koyun |
| 8 | 24 şeker, 4 kavanoza eşit pay | 24 ÷ 4 | 6 şeker/kavanoz |
| 9 | 21 gün, 1 hafta 7 gün. Kaç hafta yapar? | 21 ÷ 7 | 3 hafta |
| 10 | Dedemin 45 tarlası, 9 toruna eşit paylaştırma. | 45 ÷ 9 | 5 tarla/torun |
Bu tablo kısa bir özet sunar ancak problemleri ayrıntılı anlamak için yukarıdaki adım adım çözümleri incelemeniz önerilir.
Bölme Problemlerini Çözmek İçin İpuçları
- Problem Metnini Dikkatle Okuyun: Her soru, belirli bir senaryoya dayanır. Eklenen sayıları not edin ve hangi işlemlerin (toplama, çıkarma, bölme vb.) gerektiğini belirleyin.
- Gerekirse Toplama veya Çıkarma Kullanarak Kalan Miktarı Bulun: Bazı durumlarda önce “kalan” değeri hesaplamak gerekir (Örneğin 92 sayfalık kitabın 42 sayfası okunduğunda, kalan 50 sayfadır).
- Bölme İşleminin Anlamını Kavrayın: “Toplamı belli sayıda gruba bölmek” veya “toplamı kaçar kaçar paylaştırmak” gibi kavramlara odaklanın.
- Doğru Hesap Yapın: Özellikle 2. sınıf seviyesinde basit dört işlem hatası sahada en çok görülen sorundur. Gerekirse parmak hesabı veya küçük kağıt üzerinde basit hesaplamalar yapın.
- Uygulama ve Pekiştirme: Çok çeşitli sorular çözerek hız kazanabilirsiniz. Market alışverişi, yiyecek paylaştırma gibi örnekler, bölme işlemine hakimiyeti artırır.
Sonuç ve Özet
Bu çalışmada, “2. Sınıf Bölme İşlemi Problemleri 2” başlıklı alıştırmalarda yer alan 10 farklı bölme sorusunu ayrıntılı şekilde çözdük. Her soru için:
- Problemin anlatıldığı senaryoyu öğrendik,
- Gerekliyse ek toplama ve çıkarma işlemleriyle verileri düzenledik,
- Ardından bölme işlemini adım adım uyguladık,
- Kalansız bölme sonucuna ulaştık.
Bölme işleminin mantığı, bir miktarı eşit parçalara ayırmak üzerine kuruludur. Bu mantığı kavradığınızda; kitap sayfalarını günlük plana bölme, cevizleri kardeşler arasında pay etme, harçlıkları birleştirip ürün başına düşen maliyeti hesaplama veya hayvanların ayak sayılarından türlerini bulma gibi konuları rahatlıkla çözebilirsiniz.
Özellikle 2. sınıf düzeyinde, gerçek hayattan örnekler verildiğinde ya da paylaştırma üzerine kurulu etkinlikler yapıldığında öğrenciler daha hızlı öğrenir ve kavrarlar. İlerleyen yıllarda, bölmenin çarpma ile ilişkisini (örneğin “10 ÷ 2” işleminin “2 × ? = 10” sorusuna denk gelmesi) öğrenerek hızınızı artırabilirsiniz.
Matematik, soyut bir kavram gibi görünse de aslında hayatımızın her alanında karşımıza çıkar ve biz de bu tür basit ama etkili problemler sayesinde hem işlem pratiğini hem de mantık yürütme becerimizi geliştiririz.