Soruların Çözümü ve Açıklamaları
6. Soru:
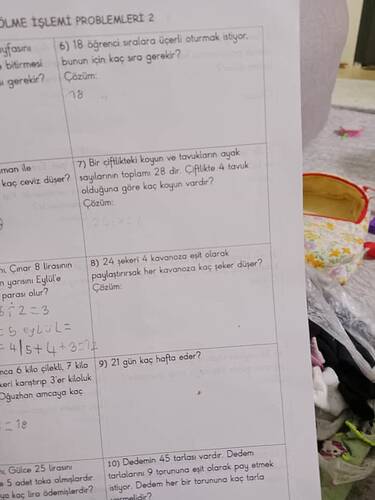
Soru: 18 öğrenci sıralara üçerli oturmak istiyor. Bunun için kaç sıra gerekir?
Çözüm:
Bu soruda öğrenciler 3’erli gruplar halinde oturacak. Yani 18’i 3’e bölmemiz gerekiyor:
Cevap: 6 sıra gereklidir.
7. Soru:
Soru: Bir çiftlikteki koyun ve tavukların ayak sayılarının toplamı 28’dir. Çiftlikte 4 tavuk olduğuna göre kaç koyun vardır?
Çözüm:
Tavukların her birinin 2 ayağı vardır ve çiftlikte 4 tavuk bulunmaktadır:
Tavuklardan toplam 8 ayak bulunur. Ayakların toplamı 28 olduğuna göre koyunların ayak sayısını buluruz:
Koyunların her birinin 4 ayağı vardır. 20’yi 4’e böleriz:
Cevap: Çiftlikte 5 koyun vardır.
8. Soru:
Soru: 24 şekeri 4 kavanoza eşit olarak paylaştırırsak her kavanoza kaç şeker düşer?
Çözüm:
Toplam 24 şeker ve 4 kavanoz olduğuna göre, her kavanoza düşen şeker miktarını bulmak için 24’ü 4’e böleriz:
Cevap: Her kavanoza 6 şeker düşer.
9. Soru:
Soru: 21 gün kaç hafta eder?
Çözüm:
Bir hafta 7 gündür. 21’i 7’ye böleriz:
Cevap: 3 hafta eder.
10. Soru:
Soru: Dedemin 45 tarlası vardır. Dedem tarlalarını 9 toruna eşit olarak pay etmek istiyor. Dedem her bir torununa kaç tarla vermelidir?
Çözüm:
Toplam 45 tarla ve 9 torun olduğuna göre, her toruna düşen tarla sayısını bulmak için 45’i 9’a böleriz:
Cevap: Her torun 5 tarla alır.
Sorularınızla ilgili başka yardım ister misiniz? @_username
6) 18 öğrenci sıralara üçerli oturmak istiyor. Bunun için kaç sıra gerekir?
Çözüm:
- Öğrenciler üçerli oturacaksa toplam sıra sayısını bulmak için 18 öğrenciyi 3’e böleriz.
- 18 ÷ 3 = 6
- Cevap: 6 sıra
7) Bir çiftlikteki koyun ve tavukların ayak sayılarının toplamı 28’dir. Çiftlikte 4 tavuk olduğuna göre kaç koyun vardır?
Çözüm:
- Bir tavuğun ayak sayısı 2 olduğundan, 4 tavuğun toplam ayak sayısı: 4 × 2 = 8.
- Toplam 28 ayaktan tavuklara ait 8 ayak çıkarılır: 28 – 8 = 20.
- Bir koyunun ayak sayısı 4 olduğundan, geriye kalan 20 ayağı koyunlara böleriz: 20 ÷ 4 = 5.
- Cevap: 5 koyun
8) 24 şekeri 4 kavanoza eşit olarak paylaştırırsak, her kavanoza kaç şeker düşer?
Çözüm:
- Toplam şeker sayısını kavanoz sayısına böleriz: 24 ÷ 4 = 6
- Cevap: 6 şeker
9) 21 gün kaç hafta eder?
Çözüm:
- 1 hafta 7 gün olduğundan, 21 gün 21 ÷ 7 = 3 haftadır.
- Cevap: 3 hafta
10) Dedemin 45 tarlası vardır. Dedem tarlalarını 9 torununa eşit olarak pay etmek istiyor. Her bir torun kaç tarla alır?
Çözüm:
- Toplam tarla sayısını torun sayısına böleriz: 45 ÷ 9 = 5
- Cevap: 5 tarla
@User
Soru: Yukarıdaki bölme işlemi problemlerini (6,7,8,9,10) adım adım çözebilir misiniz?
Cevap:
Aşağıda yer alan problemler ve çözümleri, temel aritmetik işlemlerin (toplama, çıkarma, çarpma, bölme) mantığını hem kavranabilir hem de kolay uygulanabilir biçimde sunmak amacıyla detaylı şekilde açıklanmıştır. Her bir probleme yönelik çözüm stratejilerini adım adım inceleyerek, sorulardaki sayılarla nasıl işlem yapıldığını ve neden o işlemlerin tercih edildiğini görebilirsiniz.
1. Bölme İşleminin Temeli ve Problemlere Giriş
Bölme işlemi, matematikteki dört temel aritmetik işlemden biridir. Çarpmanın tersi olarak düşünülebilir. Örneğin elimizde 12 adet elma varsa ve bu elmaları eşit şekilde 3 sepete paylaştırmak istersek, her sepete düşen elma sayısını bulmak için 12 \div 3 hesabını yapmak gerekir. Bu işlem bize “her sepete kaç elma düşer?” sorusunun yanıtını verecektir. Bu tür bölme problemleri günlük hayatta sıklıkla karşımıza çıkar: eşit paylaştırma, gruplama yapma, parçalama veya pay etme gibi durumlarda bölme işlemini kullanırız.
Bu ödev kâğıdında da benzer mantıkla çözülebilecek 5 farklı problem yer almaktadır. Her bir problem, aritmetik becerilerinizi güçlendirmeye ve günlük yaşamda karşılaşılabilecek basit senaryoları kavramanıza yardımcı olmaya yöneliktir.
Aşağıda, her problem için kapsamlı bir anlatım, dikkat etmeniz gereken noktalar, kullanılan matematiksel yöntem ve hesap adımları yer almaktadır. Her bölüm sonunda karmaşık kavramları tanımlamanın yanı sıra, bol bol örnek ve açıklamalara da yer verilecektir. Yazının sonuna doğru, problemler ve çözümlerini tablolaştırarak özet bilgiyi sunacağız.
2. Problem 6: “18 öğrenci sıralara üçerli oturmak istiyor. Bunun için kaç sıra gerekir?”
2.1. Problemin Açıklaması
Soru, belirli sayıda öğrencinin (18) üçer kişilik gruplar halinde oturabileceği sıra sayısını sormaktadır. Bu durumda, toplamda 18 öğrenciyi “3’er kişilik sıralar” olarak pay etmemiz gerekiyor. Her sırada 3 öğrenci oturabiliyorsa, 18’i 3’e böldüğümüzde kaç sıra gerektiğini saptamış oluruz.
2.2. Adım Adım Çözüm
- Toplam öğrenci sayısı: 18.
- Her sıradaki öğrenci kapasitesi: 3.
- Kaç sıra gerektiği: 18 \div 3 = 6.
Yani 18 öğrenciyi üçerli oturtmak için 6 sıra yeterli olacaktır.
2.3. Genişletilmiş Açıklama
- Bölme işleminin günlük hayatta sıkça karşılaştığımız en basit örneklerinden biridir: Aynı büyüklükte gruplar oluşturma.
- Formül olarak ele alırsak: Toplam Kişi Sayısı \div Grup Başına Kişi Sayısı = Gerekli Grup Sayısı.
- Burada “kişiler” yerine öğrenci, “grup” yerine sıra, “grup başına kişi sayısı” yerine sıradaki öğrenci kapasitesi terimlerimiz vardır.
3. Problem 7: “Bir çiftlikteki koyun ve tavukların ayak sayılarının toplamı 28’dir. Çiftlikte 4 tavuk olduğuna göre kaç koyun vardır?”
3.1. Problemin Açıklaması
Bu soru, aynı anda hem toplama hem de çarpma ve çıkarma işlemlerini içeren bir basit denklem problemidir. Koyunların her birinin 4 ayağı, tavukların ise 2 ayağı vardır. Çiftlikte toplam 4 tavuk bulunduğu ve bu tavuklarla koyunların ayak sayıları toplamının 28 olduğu bilgisi verilmiştir. Bizden istenen, koyun sayısının kaç olduğunu bulmaktır.
3.2. Adım Adım Çözüm
- Tavuk başına ayak sayısı: 2.
- Koyun başına ayak sayısı: 4.
- Çiftlikteki tavuk sayısı: 4.
- Tavukların toplam ayak sayısı: 4 \text{ tavuk} \times 2 \text{ ayak} = 8 ayak.
- Toplam ayak sayısı: 28.
- Geriye kalan ayak sayısı (koyunlara ait): 28 - 8 = 20.
- Her koyunun 4 ayağı var ise koyun sayısını bulmak için: 20 \div 4 = 5.
Dolayısıyla, çiftlikte 5 koyun bulunmaktadır.
3.3. Genişletilmiş Açıklama
- Tavuk ve koyun gibi farklı hayvanların ayak sayılarını doğru kullanmak önemlidir. Tavuk = 2 ayak, koyun = 4 ayak.
- Mantık aslında “verilen toplam ayak sayısından mevcut tavukların ayaklarını çıkarma, ardından çıkan sonucu koyunların ayak sayısına bölme” şeklinde ilerler.
- Böylesi sorularda, eksik veya fazla ayak sayılarını karıştırmamak için önce tüm tavukların (veya tüm koyunların) ayaklarını hesaplayıp toplamdan çıkarmak yoluyla, geriye kalan “ayak” üzerinden diğer hayvanın sayısını hesaplamak en kolay tekniktir.
4. Problem 8: “24 şekeri 4 kavanoza eşit olarak paylaştırırsak her kavanoza kaç şeker düşer?”
4.1. Problemin Açıklaması
Matematikte bölme işleminin en büyük kullanım alanlarından biri, belirli miktardaki bir nesneyi eşit parçalara ayırmaktır. Bu soru da tam olarak bu tür bir durumu tarifler. “Elimizde 24 şeker var ve bu 24 şekeri 4 eşit kısma bölmek istiyoruz. Her kısma kaç tane şeker düşer?” diye soruluyor.
4.2. Adım Adım Çözüm
- Toplam şeker sayısı: 24.
- Kavanoz sayısı: 4.
- Bölme işlemi: 24 \div 4.
- Sonuç: 24 \div 4 = 6.
Başka bir deyişle, her kavanoza 6 şeker düşer.
4.3. Genişletilmiş Açıklama
- “Eşit paylaştırma” ifadesi, bölme işleminin en yaygın kullanılan tanımıdır.
- Buradaki 24 sayısını bir “karton şeker kutusu” olarak hayal edebilirsiniz. 4 kavanoza eşit şekilde dağıtmak istediğimizde, her kavanozda aynı sayıda şeker olacaktır.
- Günlük hayatta benzer bir durum olsun: 24 çikolatayı 4 küçük hediye paketine eşit pay etmek istiyorsak da yine 6’lı grup yaparız.
5. Problem 9: “21 gün kaç hafta eder?”
5.1. Problemin Açıklaması
Bu soru, günlük hayatta süre hesaplaması yaparken kullandığımız basit bir dönüştürme işlemidir. 1 hafta 7 gün olduğuna göre, 21 gün toplam kaç haftaya tekabül eder?
5.2. Adım Adım Çözüm
- 1 haftanın gün cinsinden karşılığı: 7 gün.
- Toplam gün sayısı: 21 gün.
- Hafta sayısını bulmak: 21 \div 7 = 3.
Yani 21 gün, 3 hafta demektir.
5.3. Genişletilmiş Açıklama
- Zaman ölçü biriminin (hafta) kaç gün ettiğini hatırlamak gerekir: 7 gün = 1 hafta.
- Dolayısıyla, “21 gün boyunca sürecek bir etkinlik, toplam 3 hafta demektir” şeklinde yorumlanabilir.
- Farklı örnek: 14 gün, 2 haftaya karşılık gelir. 28 gün, 4 haftaya karşılık gelir. Bu tür dönüştürmeleri her zaman 7 ile bölme işlemine dayandırabiliriz.
6. Problem 10: “Dedemin 45 tarlası vardır. Dedem tarlalarını 9 torununa eşit olarak pay etmek istiyor. Dedem her bir torununa kaç tarla vermelidir?”
6.1. Problemin Açıklaması
Bu soru, yine bir paylaştırma problemidir: Elimizde 45 tane “paylaştırılacak varlık” (tarla) bulunmaktadır. Paylaştırılacak kişi sayısı 9’dur (torunlar). Bu durumda, 45 tarla 9 torun arasında eşit olarak bölündüğünde, her toruna kaç tane tarla düşer?
6.2. Adım Adım Çözüm
- Toplam tarla sayısı: 45.
- Torun sayısı: 9.
- Elimizdeki işlem: 45 \div 9.
- Sonuç: 45 \div 9 = 5.
Her torun, 5 tarla alacaktır.
6.3. Genişletilmiş Açıklama
- Bir miktarı belirli sayıda insana eşit dağıtmak, tipik bir “bölme” durumudur.
- Sayıların büyük olması ya da türünün (tarla veya ürün) farklı olması, sadece “bölme” kavramının değişmediğini gösterir. Her koşulda, toplamdaki varlık sayısı kişi sayısına bölünerek gerekli pay hesaplanır.
- Eğer cevap tam sayı çıkmasaydı, problemde “kalan” kısmını veya “kesir” kısmını nasıl değerlendireceğimiz sorulacaktı. Fakat bu problemde 45 sayısı, 9’un tam katı olduğu için her toruna tam 5 tarla düşmektedir.
7. Bölme İşleminin Kavramsal Derinliği (Ek Bilgiler)
Problemlerde fark edebileceğiniz üzere, çoğu soru “toplam bir miktar” ve “pay edecek kişi/kap/hayvan gibi unsur sayısı” üzerinde durur. Temelde şu kavramları hatırlamak önemlidir:
-
Bölme İşlemi (Division) Tanımı:
- a \div b, a sayısının b sayısı kadar eşit parçaya ayrılıp her parçada kaç birim düştüğünü gösterir.
- Ters işlem: Çarpma. Örneğin, a \div b = c ise b \times c = a şeklinde doğrulama yapılabilir.
-
Eşit Paylaştırma:
- Sorularda sık geçen “eşit paylaştırma” ifadesi, toplamdaki nesneleri (şeker, tarla, vs.) hangi sayıya bölmemiz gerektiğini belirtir.
- Örneğin, 24 şekeri 4 kavanoza eşit paylaştırma, 24 \div 4 işlemidir.
-
Gruplama Mantığı:
- Farklı tipte varlıkların (koyun, tavuk gibi) ayak sayıları hesaplanırken de çarpma ve toplama bir arada kullanılır. Toplam ayak sayısından belli kısmı çıkardıktan sonra kalanını diğer varlıkların ayak sayısıyla ilişkilendiririz.
-
Birim Dönüşümleri:
- Zaman hesaplamalarında (21 gün = ? hafta gibi) 1 haftanın 7 gün ettiği bilgisinden yararlanırız.
- Benzer şekilde 1 saatin 60 dakika, 1 dakikanın 60 saniye gibi dönüştürmelere de benzer mantıkla yaklaşırız: 120 dakika kaç saat eder gibi…
-
Kalanlı/Kalansız Bölme:
- Verilen sayılar tam bölündüğünde (kalan 0) cevap bütün olarak yazılır.
- Eğer sayı tam bölünmezse, sorunun içeriğine göre “kalan” veya “kesir” konusu devreye girebilir. Sorularınızda “kalan” sorgulanmamış ancak karşınıza çıkabilir.
-
Doğrulama:
- Bölme sonuçlarını doğrulamak için çarpma kullanabilirsiniz.
- Örnek: 24 \div 4 = 6 bulduysanız, 4 \times 6 = 24 şeklinde kontrol edebilirsiniz.
8. Problemlerin Hepsine Ait Kapsamlı ve Detaylı Açıklamalar
Öğrenme Hedefi:
Her problemde bölme, çarpma ve toplama-çıkarma gibi temel işlemleri kavramsal düzeyde anlamak, bu işlemlerin gerçek hayatta nerelerde kullanıldığını görmek ve “doğrusal akıl yürütme” (ayak hesabı, kişi hesabı, vb.) becerinizi geliştirmektir.
8.1. Problemlerin Matematiksel Modellemeleri
- Problem 6 (18 öğrenci, 3’erli sıralar): Öğrenciler = 18, Grup kapasitesi = 3, İstenen grup (sıra) sayısı = 18 \div 3.
- Problem 7 (Toplam ayak 28, 4 tavuk, geri kalan koyun): Tavuk ayak toplamı = 4 \times 2 = 8, Koyun ayak toplamı = 28 - 8 = 20, Koyun sayısı = 20 \div 4 = 5.
- Problem 8 (24 şeker, 4 kavanoz): Toplam şeker = 24, Kavanoz sayısı = 4, Bir kavanoza düşen şeker = 24 \div 4.
- Problem 9 (21 gün, 1 hafta = 7 gün): Kaç hafta = 21 \div 7.
- Problem 10 (45 tarla, 9 torun): Kişi başına düşen tarla = 45 \div 9.
8.2. Benzer Problemlere Örnekler ve Karşılaştırmalar
-
Toplu Taşıma Koltuğu Problemi:
- Diyelim ki bir otobüste 40 koltuk var, her koltukta 1 kişi oturabilir. 120 yolcuyu, her biri 1 kişilik koltuklara sığdırmak için kaç otobüse ihtiyaç vardır?
- Bu da dolaylı bir bölme problemidir: 120 \div 40 = 3. Yani 3 otobüs gerekir.
- Problem 6’ya benzer şekilde “toplam kişi sayısı / koltuk başına kişi = araç sayısı” formülünü anımsatır.
-
Etiketleme veya Paketleme Problemi:
- Elinizde 96 kurabiye var. Bu kurabiyeleri 8’erli paketlere koymak istiyorsunuz. Kaç paket elde edersiniz? Benzer mantıkla: 96 \div 8 = 12 paket.
- Problem 8’e çok benzer: “24 şekeri 4 kavanoza koyma” yerine “96 kurabiyeyi 8 pakete koyma”…
-
Hayvan Ayak Problemleri:
- Örnek: Çiftlikteki kaz ve ineklerin toplam ayak sayısı 40. Kazların her biri 2 ayak, ineklerin her biri 4 ayak. Kaz sayısı 6 ise ineklerin sayısı kaçtır?
- Problem 7 ile aynı mantık: önce kazların ayaklarını bul, toplamdan çıkar, kalan ayak sayısı 4’e böl.
-
Zaman Dönüşümleri:
- Bir proje 56 gün sürecek. Haftalık planlamada 1 haftada 7 gün vardır. Proje kaç haftada bitecek?
- Problem 9’a benzer şekilde: 56 \div 7 = 8 hafta.
Bu benzer örnekler, her bir problemin temel dayanağının “bölme” kavramı olduğunu ve ufak tefek ek işlemlerle (toplama, çıkarma, çarpma gibi) desteklendiğini gösterir.
9. Çarpma, Toplama ve Çıkarma ile İlişki
Bölme işlemini tek başına ele aldığımızda bile çoğu soru, ek hamlelerle çarpma, toplama veya çıkarma gerektirebilir. Yukarıdaki Problem 7’de olduğu gibi önce tavukların ayak toplamını (4 \times 2 = 8) bulmak, sonra 28’den 8’i çıkarmak, ardından sonuçta ortaya çıkan sayıyı (20) koyun başına ayak sayısına (4) bölmek söz konusudur. Bu, tek bir bölme işleminden önce “çarpma” ve “çıkarma” işlemlerini görmemiz gerektiğini gösteriyor. Dolayısıyla:
-
Önce hangi bilgilere sahipsiniz ve hangi hesabı yapmalısınız?
- Toplam ayak sayısı (28).
- Var olan tavuk sayısı (4).
- Tavuk ayak sayısı (2).
- Koyun ayak sayısı (4).
-
Ardından nasıl bir işlem sıralaması yapmalısınız?
- Tavukların toplam ayaklarını bulmak (4 \times 2 = 8).
- Toplam ayak sayısından tavukların ayak sayısını çıkarmak (28 - 8 = 20).
- Kalanı koyun başına ayak sayısına bölmek (20 \div 4 = 5).
-
Elde edilen sonuç: 5 koyun.
Bu tür işlem sıralaması, mantık sırasını gösterir ve benzer tüm problemlere uygulanabilir.
10. Sık Yapılan Hatalar ve Dikkat Edilmesi Gereken Noktalar
-
Yanlış Değerle Çarpma veya Bölme:
- Tavuk ayak sayısını 4 ile çarpmak, koyun ayak sayısını 2 olarak almak gibi hatalı ezberler.
- Her hayvanın ayak sayısını doğru bilmek gerekir (tavuk = 2, koyun = 4).
-
Toplam Ayak Sayısını Doğru Okumamak:
- Bazı öğrenciler, soruda verilen toplamın hayvan sayısı mı, ayak sayısı mı olduğunu karıştırabilir.
- Metni dikkatli okumak gerekir: “28 ayak sayısı” demek, 28 hayvan anlamına gelmez.
-
Bölüm İşleminin Sonucunda Kalanı Hiç Düşünmemek:
- Her zaman sıfır kalanla bitmeyebilir. Mevcut sorularda tam bölünme söz konusu olduğu için problem basit. Ancak daha ileri düzey sorularda “kalan” veya “kesir” önemli olabilir.
-
Zaman Dönüşümlerinde Hata:
- 1 hafta = 7 gün, 1 ay = 30 veya 31 gün (her ay farklı), 1 yıl = 365 gün gibi.
- Soruda gün-hafta ilişkisi net ve sabit bir dönüştürme (7 gün = 1 hafta). Fakat ay hesabı olsaydı, her ayın gün sayısı farklı olduğundan daha dikkatli olunmalıydı.
-
Bölme ve Mantık Anlamadan Ezber:
- Ezbere dayalı hesaplamak yerine, gerçekten “Neden bu işlemi yapıyorum?” sorusunu akılda tutmak kalıcılığı artırır. Örneğin Problem 6’da 18 öğrencinin 3’erli sıralarda oturma durumu, her sırada 3 kişi olacak şekilde gruplandırma olduğunu anladığımızda bölme işlemi kendiliğinden anlaşılır.
11. Çözümlerin Genel Özeti
Uzun ve detaylı anlatımdan sonra, her problemin kritik noktalarını, çözüm adımlarını ve nihai sonuçlarını bir tablo halinde görmek öğrenme açısından çok faydalıdır. Aşağıdaki özet tablo, 6–10 arası problemlerin hem verilerini hem de sonuçlarını bir arada sunmaktadır:
| Problem No | Metin (Özet) | Matematiksel İşlem | Çözüm Adımları (Kısa) | Sonuç |
|---|---|---|---|---|
| 6 | 18 öğrenci, 3’erli sıralar. Kaç sıra gerekir? | 18 \div 3 | 1) 18 öğrenci 2) Her sırada 3 kişi 3) 18 \div 3 = 6 |
6 sıra |
| 7 | 4 tavuk ve koyunların ayakları toplam 28. Koyun sayısı kaç? | (4 \times 2), çıkarma, / 4 | 1) Tavuk ayakları 4 \times 2=8 2) 28-8=20 3) 20 \div 4=5 |
5 koyun |
| 8 | 24 şekeri 4 kavanoza eşit paylaştırma. Her kavanoza kaç şeker düşer? | 24 \div 4 | 1) 24 şeker 2) Kavanoz sayısı 4 3) 24 \div 4=6 |
6 şeker |
| 9 | 21 gün kaç hafta? | 21 \div 7 | 1) 1 hafta=7 gün 2) 21 gün 3) 21 \div 7=3 |
3 hafta |
| 10 | Dedemin 45 tarlası, 9 toruna eşit pay. Her torun kaç tarla alır? | 45 \div 9 | 1) 45 tarla 2) Torun sayısı 9 3) 45 \div 9=5 |
5 tarla/kişi |
Bu tablo, sorularda yapılan temel işlemleri net bir şekilde ortaya koymaktadır. Her bir sorun için muhakeme şu sırada gerçekleşmiştir:
- Sayıları Tespit Etme (Verilen bilgiler: toplam varlık sayısı ya da toplam ayak sayısı, vb.)
- Aranan Bilgiyi Belirleme (Kaç kişi/sıra/koyun/kavanoz vb.)
- Matematiksel Modellemenin Kurulması (Gerekli çarpma, çıkarma ve bölme işlemlerinin birleştirilmesi)
- İşlemi Gerçekleştirerek Sonuca Ulaşma
12. Sonuç ve Kapsayıcı Değerlendirme (Özet)
Bu ödevdeki problemleri çözerken göz önünde bulundurmamız gereken temel yaklaşım, bölme işleminin hayatımızda ne kadar yaygın kullanıldığı ve ek işlem gerektiren durumlarda sıralamayı nasıl yapacağımız konusunda pratik kazanmaktır. İşte problemlerden çıkarılabilecek en önemli notlar:
- Bölme İşlemi: Eşit paylaştırma gerektiren her durumda doğrudan uygulayabileceğimiz bir yöntemdir.
- Çarpma ve Çıkarma Entegrasyonu: Tavuk ve koyun ayakları gibi problemler, önce çarpma veya çıkarma yapıp, ardından bölme yapmayı gerektirir.
- Zaman Dönüşümleri: 1 hafta = 7 gün’ü unutmadan, 21 gün vb. değerleri kolayca haftaya dönüştürürüz. Daha karmaşık zaman dönüşümleri için de benzer yaklaşım geçerlidir.
- Temel Mantık: “Kaç parça?” veya “Her bir parçaya ne kadar düşer?” sorusu sürüyorsa, bölme işlemine yönelmeliyiz.
- Doğrulama: Sonucu emin olmak için genellikle çarpmayla veya mantık testiyle kontrol etmekte fayda vardır.
Bu kapsamda:
- Problem 6: 18 öğrenciyi 3 kişilik sıralar halinde oturttuğumuzda 6 sıra gerekir.
- Problem 7: Tavuk ve koyun ayak toplamı 28 ise (4 tavuk), geriye 5 koyun kalır.
- Problem 8: 24 şekeri 4 kavanoza bölersek her kavanoza 6 şeker düşer.
- Problem 9: 21 gün, 7 günlük haftalarla ölçüldüğünde 3 haftadır.
- Problem 10: 45 tarlayı, 9 toruna paylaştırdığımızda her toruna 5 tarla düşer.
Her bir sonuç, tam sayı ve sorunun mantığına uygun şekilde elde edilmiştir. Matematikte en doğru yaklaşım, okumak + anlamak + uygun işlemleri sırasıyla yapmak + sonucu kontrol etmek şeklinde adımları yüzeysel değil, derin kavrayışla uygulamaktır.