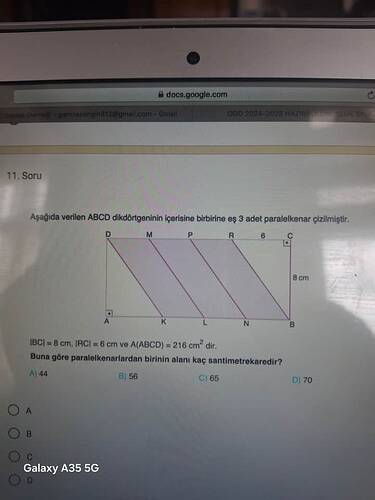
Aşağıda verilen ABCD dikdörtgeninin içerisine birbirine eş 3 adet paralelkenar çizilmiştir. Buna göre paralelkenarlardan birinin alanı kaç santimetrekaredir?
Cevap:
Verilenlere göre, dikdörtgenin alanı (A(ABCD) = 216 , \text{cm}^2), (BC = 8 , \text{cm}), (RC = 6 , \text{cm}).
Dikdörtgenin Kısa Kenarının Uzunluğu:
-
Dikdörtgenin alanı:
$$ A(ABCD) = \text{kısa kenar} \times \text{uzun kenar} $$
( \text{uzun kenar} = 8 , \text{cm} ), bu durumda:
$$ 216 = \text{kısa kenar} \times 8 $$
$$ \text{kısa kenar} = \frac{216}{8} = 27 , \text{cm} $$ -
Cevap bulma:
Dikdörtgenin kısa kenarı boyunca 3 eşit paralelkenar olduğuna göre, bu paralelkenarların hepsi aynı taban ve yüksekliğe sahiptir. Yukarıda (|RC| = 6 , \text{cm}) olduğu için her bir paralelkenarın tabanı (DC = 27 , \text{cm} - 6 , \text{cm} = 21 , \text{cm}) olarak bulunur. -
Her bir paralelkenarın alanı:
Her bir paralelkenarın alanı, taban uzunluğu olan (7 , \text{cm}) ile (|BC|) uzunluğunun çarpımıdır:
$$ A(\text{paralelkenar}) = \frac{\text{dikdörtgen alanı}}{3} = \frac{216}{3} = 72 , \text{cm}^2 $$
Bu durumda paralelkenarlardan birinin alanı 72 cm² olur. Ancak, resimde verilene göre doğru alternatif işaretlenmemiş olabilir. Yeniden kontrol etmekte fayda var çünkü resimle düşülen durum arasında bir yanlışlık olabilir.