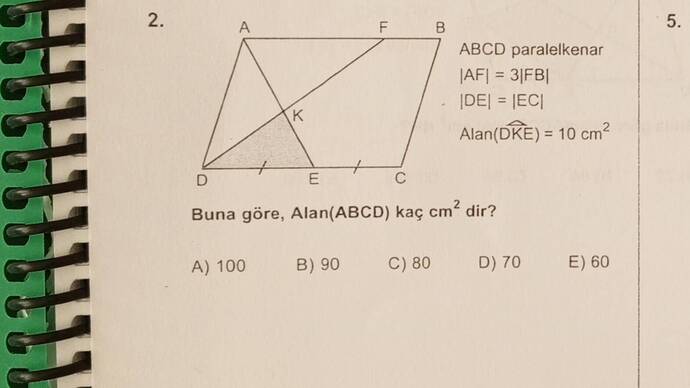
ABCD Paralelkenarının Alanı Nasıl Bulunur?
Cevap:
Verilen soruda, ABCD paralelkenarının alanı sorulmaktadır. Bilgi olarak şunları biliyoruz:
- ABCD bir paralelkenardır.
- \overline{AF} = 3\overline{FB}.
- \overline{DE} = \overline{EC}.
- \text{Alan}(DKE) = 10 \text{ cm}^2.
Şimdi bu bilgileri kullanarak alanı bulalım.
-
Paralelkenarda Alan Hesabı:
- Paralelkenarın taban uzunluğu ve yüksekliğini kullanarak alanı bulabiliriz.
- Paralelkenarın alanı, iki zıt kenarı ile bu kenarlar arasında kalan yüksekliklerden birinin çarpımı ile bulunur.
-
Bölüm Alanlarının Hesaplanması:
- Verilen bilgilere göre, \overline{DE} = \overline{EC} olduğundan DKE üçgeni, ABCDE paralelkenarının yarısının bir kısmıdır.
- \overline{AF} = 3\overline{FB} olduğundan, AB uzunluğunu \overline{AF} ve \overline{FB} oranlarına göre bölebiliriz.
-
DKE Üçgeni Alanından Yola Çıkma:
- \text{Alan}(DKE) = 10 \text{ cm}^2 verilmiştir.
- DE = EC olduğundan DKE üçgeninin alanı, paralelkenarın alanının $\frac{1}{8}$idir.
-
Paralelkenarın Alanını Bulma:
-
Verilen üçgenin alanı paralelkenarın alanının \frac{1}{8} olduğuna göre:
\text{Alan}(ABCD) = 8 \times \text{Alan}(DKE)\text{Alan}(ABCD) = 8 \times 10 = 80 \text{ cm}^2
-
Sonuç:
Paralelkenarın alanı \boxed{80} \text{cm}^2'dir.