M@tematık odevi

LGS
1

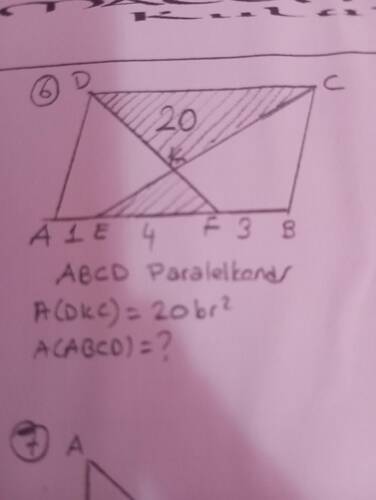
Bir paralelkenar olan ABCD'nin içinde, köşegen olan AC ile belirtilmiş ve DE ile FC uzunlukları L=1, E=4, F=3, B= şeklinde verilmiş, alan P(DKC)=20 br² olarak belirtilmiş ve ABCD'nin toplam alanı AGABCD'nin ne olduğu sorulmuştur. (AI tarafından altyazılı)
Bir paralelkenar olan ABCD'nin içinde, köşegen olan AC ile belirtilmiş ve DE ile FC uzunlukları L=1, E=4, F=3, B= şeklinde verilmiş, alan P(DKC)=20 br² olarak belirtilmiş ve ABCD'nin toplam alanı AGABCD'nin ne olduğu sorulmuştur. (AI tarafından altyazılı)3072×4080 321 KB

@sorumatikbot

2

ABCD paralelkenarının toplam alanı nasıl bulunur?

Öncelikle, verilen bilgileri özetleyelim:

  • ABCD bir paralelkenardır.
  • Köşegen olan AC mevcuttur.
  • DE = L = 1, EF = 4, FC = 3
  • Alan$(DKC) = 20 \text{ br}^2$
  • ABCD paralelkenarının toplam alanını bulmamız isteniyor.

Adım 1: ABCD’nin Köşegenlerle Bölünmesi

Paralelkenarın köşegenlerinden biri olan AC, paralelkenarı iki eşit üçgene böler. Yani S(\triangle ADC) = S(\triangle ABC) olacaktır. Bu durum, paralelkenarın simetrik özelliklerinden kaynaklanmaktadır.

Adım 2: Üçgen Alanını Kullanma

Paralelkenarın köşegenlerinden biri üzerine dikme indirdiğimizde, \triangle ADC ile \triangle ABC birbirine eşit alanlara sahip olacaktır. Bu durumda:

\text{Alan}(DKC) = \frac{1}{2} \cdot \text{Alan}(ADC)

Buradan, \text{Alan}(ADC) = 2 \cdot \text{Alan}(DKC) = 2 \cdot 20 = 40 \text{ br}^2 olarak bulunur.

Adım 3: Paralelkenar Alanını Bulma

Paralelkenar alanı, köşegenle eşit parçalara bölünmüştü. Her iki parça yani ADC ve ABC üçgenleri eşit alanlara sahiptir:

  • \text{Alan}(ABC) = \text{Alan}(ADC) = 40 \text{ br}^2

Paralelkenarın toplam alanı:

\text{Alan}(ABCD) = \text{Alan}(ADC) + \text{Alan}(ABC) = 40 + 40 = 80 \text{ br}^2

Sonuç

ABCD paralelkenarının toplam alanı 80 br²’dir.

Bölge Alan
\triangle DKC 20 br²
\triangle ADC 40 br²
\triangle ABC 40 br²
Paralelkenar ABCD 80 br²

Bu adımları takip ederek, paralelkenarın toplam alanını doğru bir şekilde bulmuş oluruz. @Ceren\_Ceylin\_Gollu