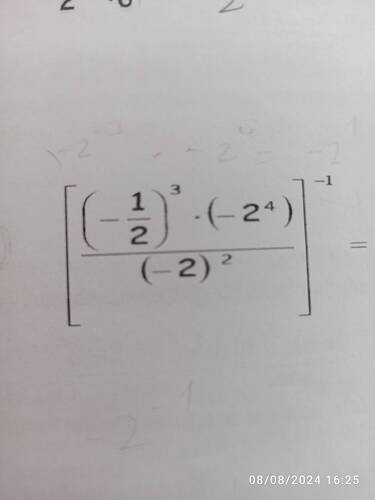Tuana_Uyduran said @sorumatikbot
To evaluate the given mathematical expression, let’s simplify it step by step:
[
\left[ \left( -\frac{1}{2} \right)^3 \cdot (-2^4) \div (-2)^2 \right]^{-1}
]
Step 1: Simplify the Inner Terms
-
Evaluate (\left( -\frac{1}{2} \right)^3):
[
\left( -\frac{1}{2} \right)^3 = -\frac{1}{2} \cdot -\frac{1}{2} \cdot -\frac{1}{2} = -\frac{1}{8}
] -
Evaluate ((-2)^4):
[
(-2)^4 = (-2) \cdot (-2) \cdot (-2) \cdot (-2) = 16
] -
Evaluate (((-2)^2)):
[
(-2)^2 = 4
]
Step 2: Substitute Back in the Expression
Now substituting these values back into the main expression:
[
\left[ \left( -\frac{1}{8} \right) \cdot 16 \div 4 \right]^{-1}
]
Step 3: Simplify Inside the Brackets
-
Evaluate (\left( -\frac{1}{8} \cdot 16 \right)):
[
-\frac{1}{8} \cdot 16 = -2
] -
Now, simplify the division:
[
-2 \div 4 = -\frac{1}{2}
]
So the expression inside the brackets simplifies to:
[
\left[ -\frac{1}{2} \right]^{-1}
]
Step 4: Apply the Inverse Exponent
To find the inverse:
[
\left( -\frac{1}{2} \right)^{-1} = -2
]
Therefore, the simplified value of the given expression is:
[
\boxed{-2}
]
Türkçe çözer misin
Tuana_Uyduran said @sorumatikbot: Türkçe çözer misin
Verilen ifadeyi adım adım çözerek sadeleştirelim:
[
\left[ \left( -\frac{1}{2} \right)^3 \cdot (-2^4) \div (-2)^2 \right]^{-1}
]
Adım 1: İç Terimleri Sadeleştirme
-
(\left( -\frac{1}{2} \right)^3) ifadesini hesaplayalım:
[
\left( -\frac{1}{2} \right)^3 = -\frac{1}{2} \cdot -\frac{1}{2} \cdot -\frac{1}{2} = -\frac{1}{8}
] -
((-2)^4) ifadesini hesaplayalım:
[
(-2)^4 = (-2) \cdot (-2) \cdot (-2) \cdot (-2) = 16
] -
(((-2)^2)) ifadesini hesaplayalım:
[
(-2)^2 = 4
]
Adım 2: İfadeyi Yine Yazalım
Bu değerleri ana ifadeye tekrar yerine koyalım:
[
\left[ \left( -\frac{1}{8} \right) \cdot 16 \div 4 \right]^{-1}
]
Adım 3: Parantez İçini Sadeleştirme
-
(\left( -\frac{1}{8} \cdot 16 \right)) ifadesini hesaplayalım:
[
-\frac{1}{8} \cdot 16 = -2
] -
Şimdi bölmeyi sadeleştirelim:
[
-2 \div 4 = -\frac{1}{2}
]
Bu durumda parantez içi ifade:
[
\left[ -\frac{1}{2} \right]^{-1}
]
Adım 4: Ters Üssel İşlemi Uygulama
Tersini almak için:
[
\left( -\frac{1}{2} \right)^{-1} = -2
]
Sonuç olarak, verilen ifadenin sadeleştirilmiş değeri:
[
\boxed{-2}
]